Certamen Nacional

Primer día

1. Hallar el número natural de 97 dígitos, todos distintos de cero, que sea múltiplo de la suma de sus 97 dígitos.

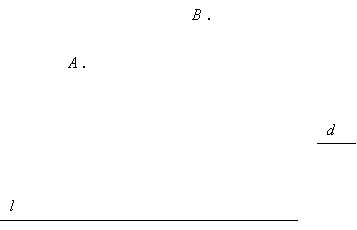
2. En la figura hay dos puntos, A y B, una recta l y un segmento de longitud d. Hallar dos puntos P y Q en la recta l de manera tal que el segmento PQ tenga longitud d y la suma AP+PQ+QB se la menor posible.

Indicar los pasos de la construcción y explicar por qué se obtuvo la menor longitud posible.

3. Sergio viaja de A hacia B y Tadeo viaja de B hacia A, los dos van a velocidades constantes y los dos inician el viaje a la misma hora. Desde el instante en que se cruzan, Sergio tarda 9 horas en llegar a B y Tadeo tarda 4 horas en llegar a A. Hallar el tiempo que tarda Sergio en su recorrido desde A hacia B y el tiempo que tarda Tadeo en su recorrido desde B hasta A.

Segundo día

4. Entre todas las fracciones a/b, con a y b números naturales, que verifican

hallar la fracción a/b que tiene el menor denominador.

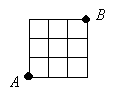
5. Un cuadrado de 3x3 se ha dividido en cuadraditos de lado 1 (ver figura). Una hormiga sale del punto A, camina por las líneas de la cuadrícula y llega a B. Los únicos puntos por los que puede pasar más de una vez son los vértices de los cuadraditos. ¿Cuál es la máxima longitud que puede tener el camino de la hormiga?

6. Sea ABCD un paralelogramo de lados AB, BC, CD y DA. Se traza por D una recta que corta al lado BC en P y a la prolongación del lado AB en Q. Si el área del cuadrilátero ABDP es 29 y el área del triángulo DPC es 8, hallar el área del triángulo CPQ.

Primer día

1. Hallar todos los números reales x que verifican

[19x + 97] = 19 + 97x.

ACLARACIÓN: Los corchetes indican la parte entera del número que encierran, por ejemplo, [3,27]=3; [1,25]=1; [-2,7]=-3; [5]=5; etc.

2. Un geólogo tiene varias piedras y ninguna de ellas pesa más de 1kg. Se sabe que si se separan las piedras en dos grupos, no importa de qué manera se haga, el peso total de uno de los dos grupos es menor o igual que 1 kg. Nada se sabe sobre la cantidad de piedras que tiene el geólogo ni se sabe cuánto pesa cada piedra. Hallar el valor máximo que puede tener el peso de todas las piedras juntas.

3. Sea ABC un triángulo acutángulo, D un punto del lado AB, E el punto del lado AC tal que DE es perpendicular a AC y F el punto del lado BC tal que DF es perpendicular a BC. Construir un punto D de manera tal que EF sea paralela a AB.

Segundo día

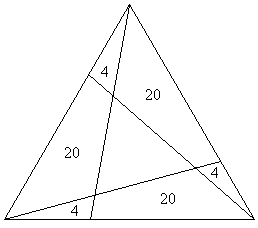
4. En la figura se muestra un triángulo equilátero dividido por tres rectas en siete regiones. En seis de las regiones se indica el área correspondiente. Hallar el área de la séptima región, es decir, del triangulito central.

5. Sea n un número natural con cuatro o más divisores naturales. De todos los divisores de n, se consideran los cuatro más pequeños: a<b<c<d.
Hallar todos los n tales que

n = a² + b² + c² + d².

ACLARACIÓN: Notar que cualquiera sea n, el divisor más pequeño es 1.

6. Se divide un triángulo equilátero de lado 10 en cien triangulitos equiláteros de lado 1, mediante paralelas a los lados del triángulo. Se elige un paralelogramo con sus cuatro vértices en vértices de triangulitos y sus cuatro lados paralelos a los lados del triángulo. ¿De cuántas maneras se puede hacer la elección del paralelogramo?

Primer día

1. Sean s y t dos rectas paralelas. Se han marcado k puntos en la recta s y n puntos en la recta t (kn). Si se sabe que la cantidad total de triángulos que tienen sus tres vértices en puntos marcados es 220, hallar todos los posibles valores de k y n.

2. Sean ABC un triángulo y M el punto medio del AB. Si se sabe que CAM+MCB=90^o, demostrar que el triángulo ABC es isósceles o es rectángulo.

3. Sean x₁, x₂, x₃, ..., x₁₀₀ cien números reales mayores o iguales que 0 y menores o iguales que 1. Hallar el máximo valor posible de la suma

S = x₁(1-x₂)+x₂(1-x₃)+x₃(1-x₄)+ ... + x₉₉(1-x₁₀₀) + x₁₀₀(1-x₁).

Segundo día

4. En el pizarrón están escritos los primeros 1997 números naturales: 1, 2, 3, ..., 1997. Delante de cada número se escribirá un signo "+" ó un signo "-", en forma ordenada, de izquierda a derecha. Para decidir cada signo, se arroja una moneda; si sale cara se escribe "+", si sale ceca, se escribe "-". Una vez escritos los 1997 signos, se efectúa la suma algebraica de la expresión que hay en el pizarrón y el resultado es S. ¿Cuál es la probabilidad de que S sea mayor que 0?

ACLARACIÓN: La probabilidad de un suceso es igual a

número de casos favorables
número de casos posibles

5. Dados en el plano dos segmentos no paralelos AB y CD, hallar el lugar geométrico de los puntos P del plano tales que el área del triángulo ABP es igual al área del triángulo CDP.

6. Decidir si existen diez números naturales y distintos a₁, a₂, ... , a₁₀ tales que

• cada uno de ellos es una potencia de un número natural con exponente natural y mayor que 1, y además
• los números a₁, a₂, ..., a₁₀ forman una progresión aritmética.

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar