Sea P en el
lado BC tal que PM
es perpendicular a QM.
Decidir si para algún valor del ángulo A
se verifica que 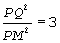
.Olimpíada
Matemática Argentina 1996Certamen Nacional
Primer nivel
Primer día
1. El desarrollo decimal de
1 / 97 tiene un período muy largo. Hallar las tres
últimas cifras del período.
2. Un auto viaja a 60 km/h
si va cuesta arriba, a 90 km/h si va cuesta abajo y a 72
km/h en los demás casos. Tarda 5 horas para ir de A
a B y 4 horas para
volver de B a A.
¿Qué longitud tiene el camino entre A
y B?
3. En un triángulo ABC,
C = 45º, Q
es el pie de la altura correspondiente al vértice B
y M es el punto medio
del lado AB.
Sea P en el
lado BC tal que PM
es perpendicular a QM.
Decidir si para algún valor del ángulo A
se verifica que ![]()
.
Segundo día
4. Sea ABC un triángulo de área 7. Se construye el triángulo XYZ de la siguiente manera: se prolonga el lado AB de modo que AXS = 2AB, se prolonga el lado BC de modo que BY = 3BC y se prolonga el lado CA de modo que CZ = 4CA. Hallar el área del triángulo XYZ.
5. Inicialmente hay un "1" en la pantalla. Al apretar la tecla A se multiplica por 3 el número de la pantalla. Al apretar la tecla B, se resta 1 al número de la pantalla. Utilizando una secuencia de teclas A y B hay que llegar a tener en la pantalla el 97. ¿Cuál es el número mínimo de teclas que se deben usar?
6. En la
lotería de Truchilandia, cada billete tiene un número
de tres cifras que usa sólo los dígitos 1, 2, 3 y 4 (se
pueden repetir los dígitos). Un billete es ganador si
coincide en por lo menos dos posiciones con el número
sorteado.
Un apostador quiere comprar varios billetes, de manera
tal que uno de ellos gane seguro, pero gastando lo menos
posible. Determinar cuántos billetes debe comprar e
indicar qué billetes debe comprar.
Aclaración: Si se sorteó el 423 entonces 123 es
un billete ganador, pero 243 no lo es.
Segundo nivel
Primer día
1. Dado un
conjunto de diez números enteros positivos no
necesariamente distintos, se realizan las siguientes diez
operaciones: se descarta el primero y se suman los nueve
restantes, se descarta el segundo y se suman los nueve
restantes y se sigue así hasta descartar el último y
sumar los nueve restantes. De esta manera se obtienen
sólo nueve resultados distintos, que son 86, 87, 88, 89,
90, 91, 92, 93, 96. Hallar los diez números iniciales.
2. Un trapecio
inscrito en una circunferencia de radio r
tiene tres lados de longitud s
y el cuarto de longitud r
+ s, con s
< r. Hallar las
medidas de los ángulos del trapecio.
3. En un tablero
de 15 x 15 Toni escribe todos los números enteros de 1
hasta 225, en ese orden, uno en cada casilla, con el
siguiente procedimiento:
En cada paso, elige la casilla en la que
escribirá el número que corresponde a ese paso y antes
de escribir ese número, suma los números que ya están
escritos en la fila y en la columna de la casilla elegida
y anota el resultado en el pizarrón; recién entonces
escribe el número que le toca en la casilla.
Cuando termina de colocar los 225 números, se
suman todos los números anotados en el pizarrón.
Indicar un procedimiento para completar el tablero de
modo que la suma del pizarrón sea la menor posible.
Segundo día
4. En el
triángulo rectángulo ABC,
B = 90o,
AB = 3, BC
= 4, AC = 5. Sea O
el baricentro del triángulo, es decir, el punto de
intersección de las medianas y sean A',
B', C'
puntos en los lados BC,
AC, AB
respectivamente, tales que OA'
es perpendicular a BC,
OB' es perpendicular a
AC y OC'
a AB. Hallar el área
del triángulo A'B'C'.
5. Se escriben
ocho números naturales distintos, uno en cada uno de los
vértices de un cubo y luego, en cada arista se escribe
el máximo común divisor de los números escritos en los
vértices correspondientes. Es posible elegir los ocho
números iniciales de manera que su suma sea igual a la
suma de los 12 números de las aristas?
6. Martín tiene
la lista de todos los números naturales de 25 cifras que
se pueden formar utilizando sólo los dígitos 1, 2, 3, 4
y tienen igual cantidad de dígitos "1" que de
dígitos "2", por ejemplo,
3333333333333333333333333, 1111111111114222222222222,
etc.
Jorge tiene la lista de todos los números
naturales de 50 cifras formados por 25 dígitos
"1" y 25 dígitos "2".
Demostrar que la lista de Martín tiene la misma
cantidad de números que la de Jorge.
Tercer nivel
Primer día
1. Se escribieron
100 números alrededor de una circunferencia. La suma de
los 100 números es igual a 100 y la suma de seis
números consecutivos es siempre menor o igual que 6. El
primer número es 6. Hallar todos los números.
2. Decidir si
existe algún número de 10 cifras tal que reordenando
10000 veces sus dígitos se obtengan 10000 números
distintos que sean múltiplos de 7.
3. El hexágono no
regular ABCDEF está
inscrito en una circunferencia de centro O
y AB = CD = EF.
Si las diagonales AC y BD se cortan en M,
las diagonales CE y DF
se cortan en N y las
diagonales AE y BF
se cortan en K,
demostrar que las alturas del triángulo MNK
se cortan en O.
Segundo día
4. Sea ABCD
un paralelogramo de lados AB,
BC, CD,
DA y centro O
tal que BAD < 90º
y AOB > 90º.
Consideremos A1 y
B1
puntos de las semirrectas OA
y OB respectivamente,
tales que A1B1
es paralelo a AB y ![]() . Demostrar que
. Demostrar que A1D
es perpendicular a B1C.
5. Determinar
todos los números reales positivos x
para los que se verifica
![]()
Aclaración: los corchetes
indican la parte entera del número que encierran; por
ejemplo, [2,16] = 2, [5] = 5, [![]() ]=1.
]=1.
6. En un torneo de
tenis de 10 jugadores, todos jugaron contra todos una
vez. En este torneo, si el jugador i
ganó el partido contra el jugador j,
entonces la cantidad total de partidos que perdió i
más la cantidad total de partidos que ganó j
es mayor o igual que 8.
Diremos que tres jugadores i,
j, k
forman un trío atípico si i
le ganó a j, j
le ganó a k y k
le ganó a i.
Demostrar que en el torneo hubo exactamente 40 tríos
atípicos.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |