II Olimpíada
Metropolitana de Matemática
Capital Federal. 7 y 8 de septiembre de 2000
| primer nivel |
1
En el pizarrón hay escritos dos números naturales de dos cifras. Nicolás multiplicó entre si los dos números del pizarrón y obtuvo un número de cuatro cifras, con la primera cifra de la izquierda igual a 2. Pedro sumó los dos números del pizarrón.
Si al número de Nicolás se le suprime la primera cifra de la izquierda, resulta un número de tres cifras, igual al número de Pedro. Determinar cuáles pueden ser los dos números del pizarrón. Dar todas las posibilidades.
2
Decidir si es posible colocar en las casillas de un tablero de ajedrez de Sxs las 16 piezas blancas y las 16 piezas negras de manera tal que para cada pieza, el número de sus,vecinas blancas sea igual al número de sus vecinas negras.
Si la respuesta es afirmativa, colocar las piezas. Si la respuesta es negativa, explicar porqué.
ACLARACION: Dos piezas son vecinas si las casillas que ocupan se tocan en un lado o en un vértice.
3
Sean ABCD un cuadrado de lados AB = BC = CD = DA = 12, E el punto medio de DA y F el punto medio de BC. Se trazan los segmentos EF, AC y BE, que dividen al cuadrado en seis regiones. Calcular el área de cada una de estas regiones.
| segundo nivel |
1
El camino entre el pueblo y el refugio en la montaña mide un número entero de kilómetros. Una mañana, tres grupos de andinistas salen del pueblo hacia el refugio. El primer día, el grupo A recorre la sexta parte del camino, el grupo B la mitad del camino, y el grupo C la cuarta parte del camino. Al día siguiente, el grupo A recorre 100 km, el grupo B recorre 10 km, el grupo C recorre 78 km, y nadie llega al refugio. Si el grupo B ha recorrido en total, más distancia que el A, pero menos que el C, determinar cuánto mide el camino desde el pueblo hasta el refugio.
2
En el cuadrado ABCD se marcan los puntos P, Q en el lado AB de manera tal que AP = PQ = QB, y se marcan los puntos R, S en el lado BC de manera tal que BR = RS = SC. Se trazan: la recta AR; la recta paralela a AR que pasa por S; la recta DP; la recta paralela a DP que pasa por Q. Estas cuatro rectas delimitan un cuadrado de área 490. Hallar la medida del lado del cuadrado ABCD.
3
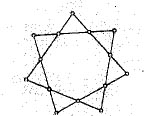
Asignar a cada uno de los puntos marcados en la figura uno de los números 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, sin repetir, de modo que en cada una de las 7 líneas la suma de los cuatro números asignados sea siempre la misma.

| tercer nivel |
1
Se escribe una lista de números de acuerdo con las siguientes reglas: en el primer paso se escribe 84; en el segundo paso se escribe 132. A partir de aquí, en cada paso se escribe el número que resulta de sumarle al último número escrito el máximo común divisor de los dos últimos números escritos. Por ejemplo, el tercer número es el resultado de 132+mcd(84;132).
¿En qué paso se escribirá por primera vez un número terminado en 7 ceros?
2
Matías debe elegir 1000 números enteros distintos entre 1 y 2000 inclusive, de modo tal que no haya entre los elegidos dos que sumen 2001, y que la suma de los 1000 números sea 1000500. Luego debe calcular la suma de los cuadrados de los 1000 números elegidos. ¿Cuántos resultados diferentes puede obtener?
3
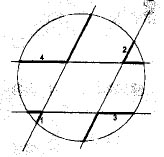
Un rombo está contenido en el interior de una circunferencia. Se prolongan cada uno de sus lados en los dos sentidos, hasta intersectar a la circunferencia; de este modo quedan determinados 8 segmentos con un vértice sobre la circunferencia y el otro coincidente con un vértice del rombo-. En la figura se indican las longitudes de cuatro de estos segmentos. Hallar la suma de las longitudes de los restantes cuatro segmentos.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |