21º Olimpíada Matemática Ñandú
Certamen Metropolitano

16 de agosto
 

Primer nivel


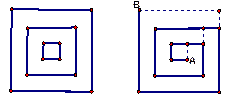
1. En la figura 1 hay 3 cuadrados: C1 de 1cm de lado, C2 de 3cm de lado y C3 de 5cm de lado; una hormiga va de A a B por el camino señalado.
    ¿Cuánto mide el camino que recorre la hormiga?                                 
    En la figura 2 hay 6 cuadrados: C1 de 1cm de lado, C2 de 3cm de lado, C3 de 5cm de lado, C4 de 7cm de lado, C5 de 9cm de lado y C6 de 11cm de lado;
    una segunda hormiga va de M a N  por un camino como el que sigue la primera hormiga.
    ¿Cuánto mide el camino que recorre la segunda hormiga?

  Figura 1

Figura 2

2. La figura, formada por un cuadrado, un rectángulo y un triángulo isósceles, tiene 96 cm de perímetro. 
    El cuadrado y el triángulo tienen igual perímetro. 
    El perímetro del rectángulo es el doble del perímetro del cuadrado.
    ¿Cuánto miden los lados del cuadrado, del rectángulo y del triángulo?

3. Esteban tiene 7 bolitas: una roja, una blanca, una negra y todas las demás azules.
    Las pone una al lado de otra en una fila, de distintas maneras pero de modo que la roja:
                    no debe estar en ninguna de las puntas de la fila y
                    no debe estar entre dos bolitas azules.
    ¿De cuántas maneras puede armar Esteban una de esas filas? Indica cuáles son.

 

Segundo nivel

1. Se dibujan estos rectángulos:


                                                                                                                    
    R1        R2             R3                   R4                       ....................

R1 de base 2cm y altura 1cm                    R2 de base 4cm y altura 1cm       
R3 de base 4cm y altura 2cm                   R4 de base 8cm y altura 2cm   
Así se siguen dibujando rectángulos: se duplica una vez la base y otra vez la altura del rectángulo anterior.      

a) Calcula el área y el perímetro del rectángulo R10.
b) ¿Cuánto suman los perímetros y cuánto suman las áreas de los 10 rectángulos?

2. En el rectángulo ABCD: AB=BC,  M es punto medio de AB, N es punto medio de BC, P es punto medio de CD y R es punto medio de AD. Si el área de ABPR es de 375 cm2,


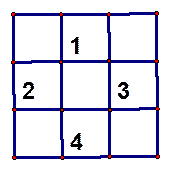
3. Los nueve casilleros del guardarropa están vacíos.
     Los numerados con 1-2-3-4 tienen puerta, los otros no.
     Ani, Ceci, Gabi y Mar guardan sus camperas, cada una en un casillero diferente.
     Siempre eligen sólo dos casilleros con puertas y, una vez elegidos los cuatro casilleros, quedan  una fila y una columna vacías,.
     ¿De cuántas maneras distintas pueden guardar sus camperas? Explica cuáles son.


Tercer nivel
 

1. En el triángulo ACE: A=90°,  AE = 2AC,  B es punto medio de AC, D es punto medio de CE y F es punto medio de AE; FD=AB.
     Los segmentos FC y BD se cortan en G.
     Si el área de ABDE es de 192 cm2,

2. ABCDEF es un hexágono regular de 3cm de lado y centro O.
   En cada uno de los triángulos AOB; BOC; COD; DOE; EOF y FOA se marca el punto de intersección de las alturas.   
   Estos puntos: M en AOB; N en BOC; P en COD; Q en DOE; R en EOF y S en FOA forman otro hexágono regular MNPQRS.
   Calcula el perímetro de MNPQRS.

3. En el micro las filas tienen 3 asientos: 2 de un lado del pasillo y 1 del otro lado.
Para los asientos de las tres primeras filas, la azafata tiene 5 paquetes de alfajores y 2 paquetes de sándwiches. Puede dejar uno o ningún paquete en cada asiento y si deja alfajores en el asiento que está solo también debe dejar alfajores en el asiento que está, en esa fila, del otro lado del pasillo.
¿De cuántas maneras distintas puede repartir los paquetes? Explica cuáles son.

 

Archivo de Enunciados Página Principal Olimpíada Matemática Argentina
   www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar