20º Olimpíada Matemática Ñandú
Certamen Metropolitano

18 de agosto
 

Primer nivel

1. Ana, Bea y Ceci ahorran para irse de excursión.
La semana pasada Ana y Bea ahorraron la misma cantidad y Ceci ahorró $8 menos que Ana y Bea juntas.
Esta semana, Ana ahorró el doble de lo que había ahorrado la semana pasada, Bea ahorró la mitad de lo que había ahorrado la semana pasada y Ceci ahorró lo mismo que la semana pasada.
Esta semana, entre las tres juntaron $ 226. ¿Cuánto ahorró cada una esta semana?

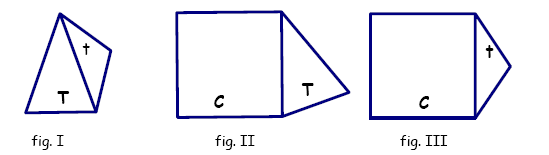
2. Con un cuadrado C y dos triángulos isósceles T y t, se armaron las figuras
siguientes:

Perímetro fig. I = 86 cm; perímetro fig. II = 140 cm;  perímetro fig. III = 126 cm.
¿Cuánto mide el lado del cuadrado?
¿Cuánto miden los lados de cada uno de los triángulos?

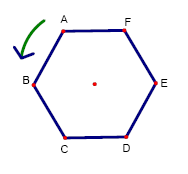
3. En los vértices del hexágono de la figura, se escriben, de menor a mayor siguiendo el sentido que señala la flecha,
todos los múltiplos de 4 menores que 2011.
Se escribe el 4 en A, el 8 en B, el 12 en C, etc.
¿Cuál es el último número que se escribe?
¿En qué vértice se escribe este número?

Segundo nivel

1. En la liquidación se ofrece: “Todas las camperas al mismo precio.” “Todos los buzos al mismo precio.” “Todos los pantalones al mismo precio.”
a) Ana hace algunos cálculos:
Si lleva dos pantalones, una campera y un buzo, paga $250 en total.
Si lleva un pantalón, dos camperas y un buzo, paga $330 en total.
Si lleva un pantalón, una campera y dos buzos, paga $260 en total.
¿Cuál es el precio de cada artículo en la liquidación?
b) Ana tiene $300 y quiere gastarlos todos, ¿cuántos artículos de cada clase
puede comprar? Da todas las posibilidades.

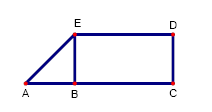
2. En la figura, BCDE es un rectángulo;
ABE es un triángulo isósceles de área 162 cm²;
BC = 2AB.
Las prolongaciones de los lados AE y CD se cortan en el punto O.
¿Cuál es el área de cada una de las siguientes figuras
• ABDE
• ABO
• BDO
• ABDO ?

3. Nico tiene una biblioteca de 6 estantes. Quiere utilizar 3 estantes para sus libros de Literatura: uno para las novelas, uno para los de cuentos y uno para los de poesías.
En los otros estantes pondrá, en uno los de Ciencias Sociales; en otro los de Ciencias Naturales y en otro los de Matemática.
Nico quiere elegir los estantes para cada clase de modo que los de Literatura estén en estantes consecutivos y los de Matemática no estén nunca en el último estante.
¿De cuántas maneras puede hacerlo? Explica cómo los contaste.

Tercer nivel
 

1. En el pueblo “Todos conectados”, el mes pasado, del total de las casas, el 50% estaban conectadas a TV por cable y a Internet, el 30% sólo estaban conectadas a TV por cable y el 20% sólo estaban conectadas a Internet.
Este mes, la sexta parte de las casas conectadas sólo a TV por cable se abonaron además a Internet; la cuarta parte de las casas conectadas sólo a Internet se abonaron además a TV por cable; las restantes no hicieron ningún cambio.
El abono mensual para ambos servicios es de $210; sólo para TV de $140 y sólo para Internet de $100.
Si todas las casas pagaran su abono, este mes se recaudarían $ 151360.
¿Cuántas casas están conectadas sólo a Internet este mes?

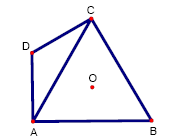
2. En la figura, ABC es un triángulo equilátero, el ángulo DAB es recto, AD = DC, O es el punto de intersección de las alturas de ABC
y el área de AOC es 46,76 cm2. ¿Cuál es el área y cuál es el perímetro del cuadrilátero ABCD?

3. Juan tiene tarjetas azules, blancas y rojas. En cada tarjeta hay escrito un número.
En las tarjetas azules están escritos todos los múltiplos de 7 entre 1 y 50.
En las tarjetas blancas están escritos todos los múltiplos de 3 entre 1 y 50.
En las tarjetas rojas están escritos todos los múltiplos de 5 entre 1 y 50.
Juan arma y desarma números poniendo tres tarjetas siempre en el mismo orden: azul – blanca – roja.
¿Cuántos números múltiplos de 3 puede obtener? Explica cómo los contaste. 

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar