I Olimpíada Metropolitana de Matemática
Capital Federal. 1999

Nivel A

1

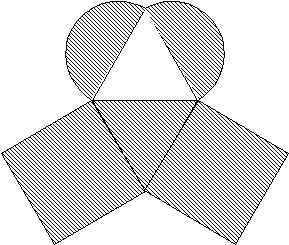
ABCD es un rombo de 384 cm2 de área.
AC = 24cm
Los arcos DC y AD son semicircunferencias.
BCEF y ANGH son cuadrados.
¿Cuál es el área de la figura rayada?

2

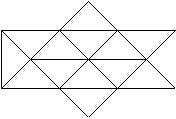
¿Cuántos polígonos convexos hay en la figura?

3

Diego, Bruno y Cristian juegan con doce fichas numeradas del 1 al 12.
Diego consigue tres fichas que sumadas dan múltiplo de 3: es un Súper-3.
Bruno consigue otras tres que, al sumar los cuadrados de sus números, dan múltiplo de 3: es un Re-Súper-3.

Cristian tiene que conseguir otra ficha que al reemplazar cualquiera de las de Diego siga siendo un Súper-3 y al reemplazar cualquiera de las de Bruno siga siendo un Re-Súper-3.

Si Cristian puede conseguir esa ficha, ¿qué fichas eligieron Diego y Bruno y cuál elige Cristian? Da todas las posibilidades.

Primer Nivel

1

Pablo reemplaza cada letra por uno de los números 1, 2, 3, 4, 5, 6, 7, 8, 9, de modo que a letras distintas le correspondan números distintos y que E + F = A, F + G = B, G + H = C, H + I = D.

Determinar los posibles valores de A + B + C + D.

2

Agustín y Bárbara salen al mismo tiempo y del mismo lugar, por el mismo camino. Agustín camina a 5km/h y Bárbara a 3km/h. Luego de recorrer 7km, Agustín emprende el regreso, y cuando se encuentra con Bárbara, también Bárbara emprende el regreso. Determinar cuánto tiempo después que Agustín llega Bárbara al punto de partida.

3

Se tiene un pentágono de papel ABCDE de lados AB, BC, CD, DE, EA, tal que AB = BC = CD, <ABC = <BCD = <DEA = 90º y AE = DE. Dividir el pentágono mediantes dos cortes rectos en tres pedazos, de modo tal que con los tres pedazos se arme un rompecabezas cuadrado. Explicar porqué al reacomodar convenientemente los tres pedazos se obtiene efectivamente un cuadrado.

Segundo Nivel

1

Un ciclista y dos atletas se entrenan en una vieja ruta rectilínea. El ciclista parte de P en dirección a Q, y al mismo tiempo, los dos atletas parten de Q en sentidos opuestos: uno se dirige hacia P y el otro se aleja de P. El ciclista los encuentra en M y en N, respectivamente, con MN = 21km. Si los atletas corren a velocidad constante de 6km/h y el ciclista va a 28 km/h, determinar la distancia PQ.

2

En el pizarrón hay escritos diez números enteros positivos consecutivos.

Laura sumó los diez números.

Matías elevó cada número al cuadrado y luego sumó los diez cuadrados obtenidos. El resultado de Matías es un múltiplo del resultado de Laura. Hallar los diez números del pizarrón. Dar todas las posibilidades.

3

Sea ABC un triángulo, con AC = BC. La bisectriz del ángulo A intersecta al lado BC en D, y la bisectrtiz del ángulo C intersecta al lado AB en E. Si AD = 2.CE, hallar la medida de los ángulos del triángulo ABC.

Tercer Nivel

1

En cada casilla de un tablero de 5x5 se debe colocar uno de los números 1, 2, 3, 4, 5, de modo que en cada fila figuren los cinco números, en cada columna figuren los cinco números y en cada diagonal figuren los cinco números. La suma de los cuatro números que quedan colocados en las cuatro casillas sombreadas es el puntaje final del juego.

a) Demostrar que es imposible obtener el puntaje 20.
b) Determinar cuál es el máximo puntaje que se puede obtener.

2

Un número a de tres cifras es raro si existe un número b de dos cifras tal que al dividir a por b, el resto es igual al cubo del cociente. Por ejemlo, 100 es raro porque al dividirlo por 46, el cociente es 2 y el resto es 8 = 2³.
¿Cuántos números raros de tres cifras hay?

3

La parábola de ecuación y = x² - ax - a, con a > 0, intersecta al eje x en los puntos P y Q y al eje y en el punto R. Sea S la circunferencia que pasa por P, Q y R, y sea T el otro punto de intersección de la circunferencia S con el eje y. Hallar las coordenadas del punto T.

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar