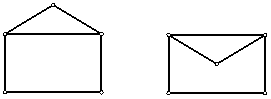18a Olimpíada Matemática Ñandú. 2009

Certamen Provincial y Metropolitano
 


Primer Nivel (versión A)

1
 Todas las semanas, Matías recibe una cuota para sus gastos.    
Una semana ahorra la mitad de la cuota de esa semana, la semana siguiente ahorra la cuarta parte de la cuota de esa semana.                                      
Así va alternando: una semana ahorra la mitad y la siguiente semana ahorra la  cuarta parte.                                                    
De este modo, en 48 semanas ahorra $ 288. ¿Cuál es su cuota semanal?     

 
2

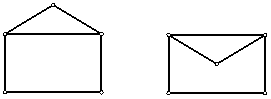    Un sobre rectangular, abierto tiene 82 cm de perímetro; cerrado su perímetro es de 80 cm. 
La solapa es triangular y tiene 50 cm de perímetro.                                                                                                         
Indica cuánto miden los lados del sobre y los de la solapa.

 

3
 Pedro tiene 15 cubos de madera, todos iguales.
Usando todos los cubos, arma y desarma torres en las que cada piso tiene una sola fila de cubos.    
Si cada piso tiene menos cubos que el anterior, indica, para cada torre, cuántos cubos hay en cada piso. Da todas las posibilidades.


Primer Nivel (versión B)
 

1
 Todas las semanas, Matías recibe una cuota para sus gastos. 
Una semana ahorra la mitad de la cuota de esa semana, la semana siguiente ahorra la tercera parte de la cuota de esa semana y la siguiente, ahorra la cuarta parte de la cuota de esa semana. 
Así va alternando: una semana ahorra la mitad, la siguiente semana ahorra la tercera parte y la siguiente, ahorra la cuarta parte. 
De este modo, en 48 semanas ahorra $ 312. ¿Cuál es su cuota semanal?     
 

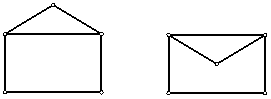    2
 Un sobre rectangular, abierto tiene 82 cm de perímetro; cerrado su perímetro es de 80 cm. 
La solapa es triangular y tiene 50 cm de perímetro.                                                                                                         
Indica cuánto miden los lados del sobre y los de la solapa.

3
Pedro tiene 15 cubos de madera, todos iguales.
Usando todos los cubos, arma y desarma torres en las que cada piso tiene una sola fila de cubos.    
Si cada piso tiene menos cubos que el anterior, indica, para cada torre, cuántos cubos hay en cada piso. Da todas las posibilidades.
 


Segundo Nivel (versión A)

1
Los chicos de quinto, sexto y séptimo grados quieren ir juntos de excursión.
 En quinto grado hay 30 chicos; en sexto, 25 y en séptimo, 20. 
 La excursión se puede hacer en micros de 50 asientos o de 30 asientos. 
La empresa cobra tantos pasajes como asientos tiene el micro, aunque no se ocupen todos.
Si usan dos micros de 50 asientos y dividen el gasto en partes iguales, cada chico debe pagar $20.
Si usan un micro de 50 asientos y uno de 30 asientos y dividen el gasto en partes iguales, a cada uno le tocará pagar $ 18.
 ¿Cuánto cuesta cada pasaje en el micro de 30 asientos?

2

En la figura:
 C es un cuadrado, T es un triángulo rectángulo y U es un triángulo isósceles rectángulo.
El área de U es 800 cm2.
El área de C es el triple del área de T.                                                                                                                                                                
¿Cuál es el área de toda la figura?

 

3
Ana escribe un número de 4 cifras.
Bea escribe el siguiente del número que escribió Ana.
La suma de los dígitos del número que escribió Ana es 25.
La suma de los dígitos del número que escribió Bea es 17.
¿Qué número pudo haber escrito Ana?
Da todas las posibilidades.

 

Segundo Nivel (versión B)

 1
Los chicos de quinto, sexto y séptimo grados quieren ir juntos de excursión.
 En quinto grado hay 30 chicos; en sexto, 25 y en séptimo, 20. 
 La excursión se puede hacer en micros de 50 asientos o de 30 asientos. 
La empresa cobra tantos pasajes como asientos tiene el micro, aunque no se ocupen todos.
Si usan dos micros de 50 asientos y dividen el gasto en partes iguales, cada chico debe pagar $20.
Si usan un micro de 50 asientos y uno de 30 asientos y dividen el gasto en partes iguales, a cada uno le tocará pagar $ 18.
 ¿Cuánto cuesta cada pasaje en el micro de 30 asientos?

2

En la figura:
C es un cuadrado, R un rectángulo, T es un triángulo rectángulo y U es un triángulo isósceles rectángulo.
El área de U es 800 cm2.
El área de C es el doble del área de R. 
El área de T es igual al área de R.
¿Cuál es el área de toda la figura?


 

3
Ana escribe un número de 4 cifras.
Bea escribe el siguiente del número que escribió Ana.
La suma de los dígitos del número que escribió Ana es 25.
La suma de los dígitos del número que escribió Bea es 17.
¿Qué número pudo haber escrito Ana?
Da todas las posibilidades.



Tercer Nivel (versión A)

1
 En diciembre del año pasado, las tres cuartas partes de los alumnos inscriptos en la escuela, eran varones.
 La inscripción se reanudó en febrero; se agregaron 105 varones y 195 mujeres.
El número de mujeres representaba, a fin de febrero, la tercera parte de los inscriptos hasta ese momento.                                                       
¿Cuántas mujeres había inscriptas en diciembre?

 2
 En la circunferencia de centro O,

  - los arcos EF, FG y GE son iguales, cada uno de 25,12 cm de longitud,

  - el arco GH es igual al arco HE.

  ¿Cuál es el área de EFGH?

 

 
3
 Juan escribe una lista de 15 números en la que:
      - el cuarto número es 5,
     - el décimo número es 10,
     - el último número es 22,    
     - siempre que se suman cuatro números consecutivos de la lista, se obtiene 215. ¿Cuál es la lista de números que escribió Juan?

 

Tercer Nivel (versión B)

1
 En diciembre del año pasado, las tres cuartas partes de los alumnos inscriptos en la escuela, eran varones.
 La inscripción se reanudó en febrero; se agregaron 105 varones y 195 mujeres.
El número de mujeres representaba, a fin de febrero, la tercera parte de los inscriptos hasta ese momento.                                                       
¿Cuántas mujeres había inscriptas en diciembre?

 2
Sobre una circunferencia de centro O, se marcan los puntos E,F,G y H de modo que los arcos GH y HE son iguales,
los arcos EF y FG son ambos iguales al doble del arco GH.

   La longitud del arco EF es 25,12 cm. El punto A está alineado con F y G.
   El punto D está alineado con F y E.
   ABHG y CDEH son cuadrados.
   El triángulo BCH es equilátero.
   ¿Cuál es el área de ABCDF?


 

 

       3
Juan escribe una lista de 17 números enteros en la que:
      - algún número es el doble de otro,
     - el cuarto número es 5,
     - el décimo número es 30,
     - el último número es 21,
     - siempre que se suman cinco números consecutivos de la lista, se obtiene 215.
 ¿Cuál es la lista de números que escribió Juan?
¿Hay más de una? En caso afirmativo, da todas las posibles.