15^a Olimpíada Matemática Ñandú. 2006

Certamen Provincial y Metropolitano

Primer Nivel

1 La cooperadora de la escuela compró libros de cuentos. 
Por una promoción le regalaron 1 libro por cada docena de libros que compró. Le enviaron 273 libros en total. 
 Compró libros de $ 8 y libros de $ 4. Pagó $ 1536 en total. 
 ¿Cuántos libros le regalaron?  ¿Cuántos libros de $ 8 y cuántos libros de $ 4 compró?

2 La figura está partida en un cuadrado, un rectángulo y un triángulo. 
 CD = DE 
El perímetro de BCDEF es 6 cm más que el perímetro del triángulo CDE.  
El perímetro del rectángulo ACEG es 38 cm. 
El perímetro de la figura es 50 cm.
¿Cuánto mide cada uno de los lados de BCDEF?

3  Camila dibujó un triángulo equilátero.  
Marcó los vértices y, sobre cada lado, marcó dos puntos.  
¿Cuántos triángulos que tengan sus tres vértices en los puntos marcados puede dibujar?

Segundo Nivel

1  En la final de un campeonato mundial de rugby, las dos terceras partes de los espectadores son residentes locales y el resto, extranjeros.   Cada uno de los espectadores simpatiza con uno de los dos equipos que se  enfrentan: los Pumas y los Canguros.  Entre los residentes locales, la cuarta parte simpatiza con los Pumas.  Hay 31080 simpatizantes de los Canguros entre los residentes locales.  Entre los extranjeros, las tres quintas partes simpatizan con los Canguros.  ¿Cuántos espectadores hay en total? ¿Cuántos simpatizan con los Pumas?

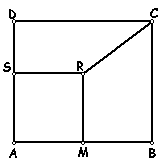
2  En la figura:  ABCD es un rectángulo,  AMRS es un cuadrado,   M es punto medio de AB. 
 El área de ABCD es 224 cm2, el área de SRCD es 72 cm2 y  el perímetro de SRCD es 40 cm. 
 ¿Cuál es el área de MBCR y  cuál es el perímetro de MBCR?

3 En una oficina hay 7 empleados Agustín, Benjamín, Carlos, Diego, Enrique, Federico y Gustavo.  
Hoy decidieron intercambiar sus lugares de trabajo de modo que,  cuatro se quedaron en su propio escritorio y  ninguno de los otros tres está en su propio escritorio.
 ¿De cuántas maneras pueden haberse ubicado para trabajar?

Tercer Nivel

1  Un comerciante vendió: las dos quintas partes de su mercadería perdiendo el 8 % y la mitad de lo que le quedaba ganando el 4 % .  
Si quiere ganar el 10 % sobre el total, ¿con qué porcentaje de ganancia debe vender lo que le queda?

2   En el triángulo equilátero ABC se marcan  los puntos M, N, O, P, S y T de modo que los triángulos MAN, OBP y SCT  son equiláteros e iguales entre sí.  
NO = 2 AN.  
Uniendo los puntos medios de MN, OP y ST  se dibuja el triángulo equilátero XYZ. 
Si el perímetro de ABC es 96 cm,  ¿cuál es el área de la parte sombreada?

3    En el pizarrón están escritos los dígitos del 1 al 9.  Iñaki escribe todos los conjuntos de 7 números distintos, elegidos entre los  que están en el pizarrón.   
Rodrigo pinta de rojo el mayor de los números de cada uno de los  conjuntos que escribió Iñaki. Ana suma todos los números pintados de rojo.
¿Cuánto vale la suma de Ana?

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar