Primer Nivel

1. En un tablero cuadrado con 9 casillas (de tres por tres) se deben colocar nueve elementos del conjunto S={0, 1, 2, 3, 4, 5, 6, 7, 8, 9}, diferentes entre sí, de modo que cada uno esté en una casilla y se cumplan las siguientes condiciones:

• Las sumas de los números de la segunda y tercera fila sean, respectivamente, el doble y el triple de la suma de los números de la primera fila.
• Las suma de los números de la segunda y tercera columna sean, respectivamente, el doble y el triple de la suma de los números de la primera columna.

Mostrar todas las formas posibles de ubicar elementos de S en el tablero, cumpliendo con las condiciones indicadas.

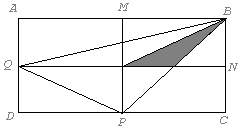
2. En el rectángulo ABCD, M, N, P y Q son los puntos medios de los lados. Si el área del triángulo sombreado es 1, calcular el área del rectángulo ABCD.

3. En un tablero de 8 por 8, se han colocado 10 fichas que ocupan, cada una, una casilla.
En cada casilla sin ficha , está escrito un número entre 0 y 8, que es igual a la cantidad de fichas colocadas en sus casillas vecinas. Casillas vecinas son las que tienen un lado o un vértice en común.

Dar una distribución de las fichas que haga que la suma de los números escritos en el tablero sea la mayor posible.

4. Joaquín y su hermano Andrés, van todos los días a clase en el autobús de la línea 62. Joaquín paga siempre los boletos.
Cada boleto tiene impreso un número de 5 dígitos. Un día, Joaquín observa que los números de sus boletos - el suyo y el de su hermano - además de consecutivos, son tales que la suma de los diez dígitos es precisamente 62.
Andrés le pregunta si la suma de los dígitos de alguno de los boletos es 35 y, al saber la respuesta, puede decir directamente el número de cada boleto.

¿Cuáles eran esos números?

5. Cuando Pablo cumple 15 años, celebra una fiesta invitando a 43 amigos. Les presenta una torta (pastel) en forma de polígono regular de 15 lados y sobre ella 15 velas.
Las velas se disponen de modo que entre velas y vértices nunca hay tres alineados (tres velas cualesquiera no están alineadas, ni dos velas cualesquiera con un vértice del polígono, ni dos vértices cualesquiera del polígono con una vela).
Luego Pablo divide la torta en trozos triangulares, mediante cortes que unen velas entre sí o velas y vértices, pero que además no se cruzan con otros ya realizados.

¿Por qué, al hacer esto, Pablo pudo distribuir un trozo a cada uno de sus invitados pero él se quedó sin comer?

Segundo Nivel

1. ¿Cuántos números de siete dígitos son múltiplos de 388 y terminan en 388?

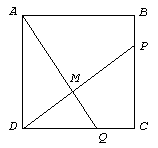
2. En un cuadrado ABCD de lado k, se ubican los puntos P y Q sobre los lados BC y CD respectivamente, de tal manera que PC = 3PB y QD = 2QC. Si se llama M al punto de intersección de AQ y PD, determinar el área del triángulo QMD en función de k.

3. Se tienen 10000 fichas iguales con forma de triángulo equilátero.

Con estos triangulitos se forman hexágonos regulares, sin superposiciones ni huecos. Si se forma el hexágono regular que desperdicia la menor cantidad posible de triangulitos, ¿cuántos triangulitos sobran?

4. En las figuras, se señalan los vértices con un círculo. Se llaman caminos a los segmentos que unen vértices. Se distribuyen números enteros no negativos en los vértices y, en los caminos, las diferencias entre los números de sus extremos.

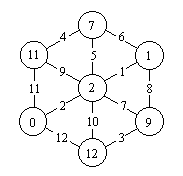
Diremos que uina distribución de números es garbosa si aparecen en los caminos todos los números de 1 a n, donde n es el número de caminos.

El siguiente es un ejemplo de distribución garbosa:

Dar -si es posible- una distribución garbosa para las siguientes figuras. En caso de no poder hacerlo, mostrar por qué.

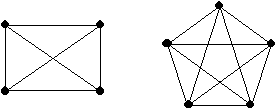
5. ¿Cuáles son las posibles áreas de un hexágono con todos los ángulos iguales y cuyos lados miden 1, 2, 3, 4, 5 y 6, en algún orden?

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar