XIV Olimpíada de Mayo

Mayo de 2008

¿Cuántos números distintos de 6 cifras y múltiplos de 45 se pueden escribir añadiendo un dígito a la izquierda y otro a la derecha de 2008?

PROBLEMA 2

En el colegio Olímpico los exámenes se califican con números enteros, la menor nota posible es 0, y la mayor es 10. En la clase de aritmética el profesor toma dos exámenes. Este año tiene 15 alumnos. Cuando uno de sus alumnos obtiene en el primer examen menos de 3 y en el segundo examen más de 7, él lo llama alumno superado . El profesor, al terminar de corregir los exámenes, promedió las 30 notas y obtuvo 8. ¿Cuál es la mayor cantidad de alumnos superados que pudo haber tenido esta clase?

PROBLEMA 3

En un pizarrón están escritos todos los números enteros del 1 al 2008 inclusive. Se borran dos números y se escribe su diferencia. Por ejemplo, si se borran 5 y 241, se escribe 236. Así se continúa, borrando dos números y escribiendo su diferencia, hasta que sólo queda un número. Determina si el número que queda al final puede ser 2008. ¿Y 2007?
En cada caso, si la respuesta es afirmativa indica una secuencia con ese número final, y si es negativa, explica por qué.

PROBLEMA 4

Sobre el lado AB de un cuadrado ABCD se dibuja exteriormente el triángulo rectángulo ABF , de hipotenusa AB . Se sabe que AF = 6, y que BF = 8. Llamamos E al centro del cuadrado. Calcula la longitud de EF .

PROBLEMA 5

En un tablero de 16 x 16 se colocaron 25 monedas, como en la figura. Está permitido seleccionar 8 filas y 8 columnas y retirar del tablero todas las monedas que se encuentran en esas 16 líneas. Determina si es posible retirar todas las monedas del tablero.

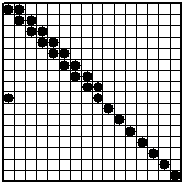
Si la respuesta es afirmativa, indica las 8 filas y las 8 columnas seleccionadas, y si es negativa, explica por qué.

PROBLEMA 1

En el pizarrón está escrita la siguiente expresión

.

Juan intercala paréntesis de distintas maneras y efectúa el cálculo que queda. Por ejemplo así o así

.

¿Cuántos resultados diferentes puede obtener Juan?

PROBLEMA 2

En el rectángulo ABCD de lados AB , BC , CD y DA , sea P un punto del lado AD tal que .

La perpendicular a BP trazada por A corta a BP en M y la perpendicular a CP trazada por D corta a CP en N .

Demuestra que el centro del rectángulo está en el segmento MN .

PROBLEMA 3

En los números se alternan unos y ceros; si hay n unos, hay n – 1 ceros ( ).

Determina los valores de n para los cuales el número , que tiene n unos, es primo.

PROBLEMA 4

En el plano se tienen 16 rectas tales que no hay dos paralelas ni tres concurrentes. Sebastián tiene que colorear los 120 puntos que son intersección de dos de las rectas de modo que en cada recta todos los puntos sean de distinto color.

Determina el mínimo número de colores que necesita Sebastián para su tarea.

¿Y si las rectas son 15 (en este caso, los puntos son 105)?

PROBLEMA 5

Matías cubrió un tablero cuadrado de 7 × 7, dividido en casillas de 1 × 1, con piezas de los siguientes tres tipos

sin huecos ni superposiciones, y sin salirse del tablero.

Cada pieza del tipo 1 cubre exactamente 3 casillas y cada pieza del tipo 2 o del tipo 3 cubre exactamente 4 casillas.

Determina la cantidad de piezas del tipo 1 que pudo haber usado Matías.

(Las piezas se pueden girar y dar vuelta.)

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar