41º Olimpíada Internacional de Matemática

Corea del Sur - 15 al 25 de julio de 2000

PRIMER DÍA (19/07/00)

1

Dos circunferencias G₁ y G₂ se cortan en M y N. Sea l la tangente común a G₁ y G₂ tal que M está más cerca de l que N. La recta l es tangente a G₁ en A y a G₂ en B. La recta paralela a l que pasa por M corta de nuevo a G₁ en C y a G₂ en D. Las rectas CA y DB se intersectan en E; las rectas AN y CD se intersectan en P; las rectas BN y CD se intersectan en Q.

Demostrar que EP = EQ.

2

Sean a, b, c números reales positivos tales que abc = 1. Demostrar que

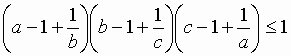
3

Sea n > 2 un número entero positivo. Inicialmente hay n pulgas en una recta horizontal, y no todas están en el mismo punto. Para un número real positivo l, definimos un salto como sigue:

Se eligen dos pulgas cualesquiera situadas en puntos A y B con A a la izquierda de B;

Luego, la pulga situada en A salta hasta el punto C de a recta, ubicado a la derecha de B, tal que BC / AB = l.

Determinar todos los valores de l tales que, para cualquier punto M de la recta y cualesquiera posiciones iniciales de las n pulgas, existe una sucesión finita de saltos que permite situar a todas las pulgas a la derecha de M.

SEGUNDO DÍA (20/07/00)

4

Un mago tiene cien tarjetas numeradas del 1 al 100. Las coloca en tres cajas, una roja, una blanca y una azul, de modo que cada caja contiene por lo menos una tarjeta.

Una persona del público selecciona dos de las tres cajas, elige una tarjeta de cada una, y anuncia a la audiencia la suma de los números de las dos tarjetas elegidas. Al conocer esta suma, el mago identifica la caja de la cual no se eligió ninguna tarjeta.

¿De cuántas maneras se pueden distribuir todas las tarjetas en las cajas de modo que este truco siempre funcione?

(Dos maneras de distribuir se consideran distintas si hay al menos una tarjeta que es colocada en una caja diferente en cada distribución.)

5

Determinar si existe un entero positivo n tal que

exactamente 2000 números primos diferentes dividen a n, y

n divide a 2ⁿ + 1

6

Sean AH₁, BH₂, CH₃ las alturas de un triángulo acutángulo ABC. La circunferencia inscrita en el triángulo ABC es tangente a los lados BC, CA, AB en los puntos T₁, T₂, T₃ respectivamente.

Sea l₁ la recta que es simétrica a H₂H₃ con respecto a T₂T₃, l₂ la recta que es simétrica a H₃H₁ con respecto a T₃T₁, l₃ la recta que es simétrica a H₁H₂ con respecto a T₁T_2.

Demostrar que l₁, l₂, l₃ determinan un triángulo cuyos vértices son puntos de la circunferencia inscrita en el triángulo ABC.

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar