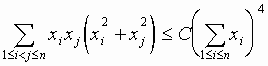
40º Olimpíada Internacional de Matemática
16 y 17 de Julio de 1999. Bucarest, Rumania.

PRIMER DÍA (16/07/99)

1

Determinar todos los conjuntos finitos S de puntos del plano que tienen por lo menos tres puntos y satisfacen la siguiente condición:

"Para cualesquiera dos puntos distintos A y B de S, la mediatriz del segmento AB es un eje de simetría de S".

2

Sea n > 2 un entero dado.

Determinar la menor constante C para la cual se verifica la desigualdad:

para todos los números reales x₁, x₂, ... x_n > 0

Para esta constante C, determinar cuándo se verifica la igualdad.

3

Se considera un tablero cuadrado de n x n, donde n es un entero positivo par. El tablero se divide en n² cuadrados unitarios. Decimos que dos cuadrados distintos del tablero son adyacentes si tienen un lado en común.

Se marcan N cuadrados unitarios del tablero de tal manera que cada cuadrado (marcado o sin marcar) es adyacente a por lo menos un cuadrado marcado.

Determinar el menor valor posible de N.

SEGUNDO DÍA (17/07/99)

4

Determinar todas las parejas (n,p) de enteros positivos tales que:

p es primo,

n < 2p, y

(p - 1)ⁿ + 1 es divisible por n ^p-1

5

Dos circunferencias G₁ y G₂ están dentro de la circunferencia G , y son tangentes a G en los puntos distintos M y N respectivamente. La circunferencia G₁ pasa por el centro de la circunferencia G₂. La recta que pasa por los dos puntos de intersección de G₁ y G₂ corta a G en los puntos C y D respectivamente.

Demostrar que CD es tangente a G₂.

6

Determinar todas las funciones f : R --> R tales que

f (x - f (y)) = f ( f (y)) + xf (y) + f (x) - 1

para todos x, y Î R.

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar