4. Determinar
todos los enteros positivos n
tales que n no es un
cuadrado perfecto y n2
es múltiplo de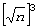 
.XXXVIII
Olimpíada Internacional de Matemática.Prueba de selección
1. ¿Cuántos números
reales x, 0 < x
< 1997, verifican que x2-4x
es un número entero?
2. Sea ABC
un triángulo isósceles con AC=BC.
Sea O el centro de la
circunferncia circunscrita al triángulo e I
el centro de la circunferencia inscrita en el triángulo.
Si D es el punto del
lado BC tal que OD
es perpendicular a BI,
demostrar que ID es
paralelo a AC.
3. Hallar todas
las funciones f: IR
-> IR tales que
f(x.f(x)
+ f(y))=(f(x))2
+ y
para todos los valores reales de x
e y.
4. Determinar
todos los enteros positivos n
tales que n no es un
cuadrado perfecto y n2
es múltiplo de .
5.
Sea ABCDE un
pentágono regular y X
un punto interior tal que <AEX
= 48o y <BCX
= 42o. Hallar <AXC.
( <ABC
es el ángulo ABC )
6.
Hay n autos, numerados
de 1 a n y una hilera
de n lugares para
estacionar, numerados de 1 a n.
Cada auto i tiene su
lugar preferido a1;
cuando quiere estacionar se dirige a dicho lugar, si
está libre estaciona y si está ocupado avanza hasta
encontrar el primer lugar libre y estacionar allí. Si no
encuentra lugar de este modo, se va y no regresa más.
Determinar cuántas sucesiones de lugares preferidos a1,
a2,
..., an
hay tales que todos logran estacionar.
Aclarción:
Autos distintos pueden tener el mismo lugar preferido.
 Archivo de
Enunciados Página
Principal |
Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
| mensajes webmaster@oma.org.ar |