Primer día

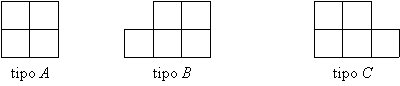
1. Se cubre completamente un tablero cuadriculado de 1993 x 1994 casillas con fichas de los siguientes tipos

¿Cuál es el máximo número de fichas tipo A que pueden intervenir en el cubrimiento?

Aclaración: Las fichas del tipo B o del tipo C pueden ubicarse en cualquiera de las cuatro posiciones

2. En un triángulo ABC, sea H el pie de la altura trazada desde A. La bisectriz del ángulo B corta al lado AC en E y el ángulo BEA es de 45 grados. Calcular la medida del ángulo EHC.

3. Para cada entero positivo k sea d(k) el mayor número impar que divide a k. Si D(n)=d(1)+d(2)+... .+d(n) y T(n)=1+2+... +n, demostrar que existen infinitos enteros positivos n para los cuales:

3.D(n)=2.T(n)

4. Se escriben en forma sucesiva enteros positivos a₁,a₂,a₃,... , con la siguiente condición:

el número a_n+1 que se elige a continuación de a₁,a₂,a₃,... ,a_n NO se puede expresar como suma de los enteros anteriores, tomando cada uno de ellos una, varias o ninguna vez. Es decir, a_n+1 NO es de la forma k₁.a₁+k₂.a₂+... +k_n.a_n con k₁,k₂,... ,k_n enteros no negativos.

¿Es posible que este proceso sea infinito? Justificar.

5. Sea Q⁺el conjunto de los números racionales mayores que cero. Hallar todas las funciones f:Q⁺--> Q⁺que satisfacen simultáneamente las siguientes condiciones:

1. f(x+1)=f(x)+1 para todo x.
2. f(x³)=(f(x))³ para todo x.

6. Sea n un número natural. A cada subconjunto del conjunto {1,2,3,... ,n} se le asigna un número natural entre 1,2,3,... ,n.

Demostrar que hay dos subconjuntos A y B a los que se les ha asignado un mismo número y ademas dicho número es el máximo de los que están en A Union B pero no están en A Intersección B.

Aclaración: el conjunto vacío y {1,2,... ,n} son subconjuntos de {1,2,... n}.

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar