VII Olimpíada Iberoamericana de Matemática

Septiembre de 1992. Caracas, Venezuela

1

Para cada entero positivo n, sea a_n el último dígito del número. 1+2+3+...+n Calcular a₁ + a₂ + a₃ + ... + a₁₉₉₂.

2

Dadas la colección de n números reales positivos a₁ < a₂ < a₃ < ... < a_n y la función

Determinar la suma de las longitudes de los intervalos, disjuntos dos a dos, formados por todos los x = 1.

3

En un triángulo equilátero ABC cuyo lado tiene longitud 2 se inscribe la circunferencia G.

1. Demostrar que para todo punto P de G, la suma de los cuadrados de sus distancias a los vértices A, B y C es 5.
2. Demostrar que para todo punto P de G es posible construir un triángulo cuyos lados tienen las longitudes de los segmentos AP, BP y CP, y que su área es:

/4

4

Sean (a_n) y (b_n) dos sucesiones de números enteros que verifican las las siguientes condiciones:

1. a₀ = 0, b₀ = 8

2. a₁ = 2

3. a_n es un cuadrado perfecto para todo n. Encontrar un número N de cinco cifras diferentes y no nulas, que sea igual a la suma de todos los números de tres cifras distintas que se pueden formar con cinco cifras de N.

5

Se da la circunferencia C y los números positivos h y m de modo que existe un trapecio ABCD inscrito en C, de altura h y en el que la suma de las bases AB y CD es m. Construir el trapecio ABCD.

6 A partir del triángulo T de vértices A, B y C se construye el hexágono H de vértices A1, A2, B1, B2, C1, C2 como se muestra en la figura. Demostrar que: área(H) 13.área(T)

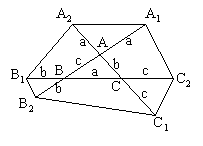Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar