22° Olimpíada Iberoamericana de Matemática
Prueba de Selección

9 y 10 de agosto de 2007

Primer día

1. Determinar todos los enteros positivos a, b, c, d,e tales que a > b > c > d > e y

.

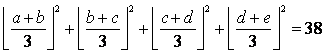ACLARACIÓN: denota la parte entera de x, es decir, el mayor entero que es menor o igual quex.

2. Sean m > 1 y n > 1 enteros impares. En cada casilla de un tablero de mxn se escribe un número distinto (son en total mn números). Diremos que un número es importante si es el mayor de su fila y, al mismo tiempo, es justo el número del medio entre todos los de su columna o si es el mayor de su columna y, al mismo tiempo, es justo el número del medio entre todos los de su fila.
Determinar cuál es la mayor cantidad de números importantes que puede tener el tablero.
ACLARACIÓN: Si m es impar, el número justo del medio de m números distintos es el que tiene, entre esos m números, números mayores que él y  números menores que él.

3. En un triángulo ABC, con AB <BC, sea D en el lado AC tal que AB = BD. Sean K y L los puntos de tangencia de la circunferencia inscripta en el triángulo ABC con los lados AB y AC, respectivamente, y sea J el incentro del triángulo BCD. Demostrar que el punto de intersección de KL y AJ es el punto medio del segmento AJ.

Segundo día

4. Sean A, B, C, D, E cinco puntos de una circunferencia G tales que el pentágono ABCDE es convexo. Se sabe que AD es un diámetro de G y que las diagonales BE y AC son perpendiculares. Sea P el punto donde se cortan CE y AD.
Demostrar que

área(APE) = área(ABC) + área(CDP).

5. Demostrar que si N es un número natural que no es divisible por 81 y se puede representar como , con a, b y c enteros divisibles por 3, entonces N también se puede representar como , de modo que x, y, z sean números enteros y ninguno de ellos sea divisible por 3.

6. Se considera un tablero de 10x10 dividido en cuadritos de 1x1. En cada paso se eligen dos filas y dos columnas del tablero, y se colorean los 4 cuadritos de 1x1 que están en la intersección de esas dos filas y esas dos columnas. El paso es legítimo si al menos uno de los 4 cuadritos de 1x1 no estaba coloreado previamente. Determinar el mayor número de pasos legítimos que se pueden realizar hasta que el tablero quede totalmente coloreado.

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar