17° Olimpíada Iberoamericana de Matemática
Prueba de Selección

22 y 23 de agosto de 2002

Primer día

1. Se tiene un triángulo equilátero de lado 33 subdividido mediante paralelas a sus lados en 33²=1089 triangulitos equiláteros de lado 1. Se debe colorear de rojo algunos segmentos de longitud 1 que sean lados de triangulitos, de manera tal que ningún triangulito resulte con sus tres lados rojos. Determinar la máxima cantidad de segmentos de longitud 1 que se puede colorear de rojo.

2. En un cuadrilátero convexo ABCD (que no es un paralelogramo) las diagonales AC y BD se cortan en P. La bisectriz del ángulo  intersecta al lado AB en Q y la bisectriz del ángulo intersecta al lado AD en R.

Denotamos M y N a los puntos medios de AC y BD respectivamente y sea O el punto de MN tal que.

Demostrar que la recta AO pasa por el punto medio deQR.

3. Se considera la suma de 1023 sumandos

.

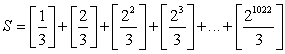Sea la sucesión de 0 y 1 formada, respectivamente, por los coeficientes de en el desarrollo binario de S. Hallar la sucesión

Aclaración: Los corchetes indican la parte entera del número que encierran.

Segundo día

4. En cierto país solamente hay monedas de 2 y de 3 centavos, y la entrada al cine cuesta 1 centavo. Un grupo de n amigos fue al cine. En la puerta, cada uno puso todas las monedas que tenía en un “fondo común”. Con las monedas reunidas, se pagaron las n entradas, sin recibir vuelto del cajero, y luego se distribuyeron las monedas sobrantes de modo que cada uno recibió la cantidad de dinero correcta, es decir, 1 centavo menos de los que había puesto. Determinar, para cada n, la mínima cantidad de dinero que podía tener el “fondo común”.

5. Hallar todas las soluciones reales de la ecuación

.

Aclaración: Las llaves indican la parte decimal del número que encierran, es decir,, donde  es la parte entera de a.

6. Determinar el mínimo número real r tal que sea posible cubrir un triángulo equilátero de lado 1 con seis círculos de radior.

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar