32=9,
32+1=27 y 9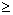 2+7=9
2+7=9Prueba
de selección para la XII Olimpíada Iberoamericana de
Matemática22/8/97 Primer día
1. Sean ABCD
un paralelogramo (AB||CD y BC||AD)
y O un punto interior
tal que AOB+COD=180o.
Demostrar que OBC=ODC.
2. Un número
natural n es atrevido
si la suma de las cifras de 3n
es mayor o igual que la suma de las cifras de 3n+1.
Por ejemplo, 2 es atrevido pues
32=9,
32+1=27 y 9![]() 2+7=9
2+7=9
11 es atrevido pues
311=177147,
311+1=531441 y
27=1+7+7+1+4+7![]() 5+3+1+4+4+1=18.
5+3+1+4+4+1=18.
Demostrar que hay infinitos números atrevidos.
3. La computadora
de Fabio tiene un programa tal que al apretar la tecla
"F" transforma al número natural N
escrito en la pantalla de acuerdo con las siguientes
reglas:
Si N es
impar, entonces N=2n-1
y lo reemplaza por 2n.
Si N es par,
entonces N=2n
y lo reemplaza por n+(2n/d(n)),
donde d(n) es el mayor
divisor impar de n.
Inicialmente el número escrito en la pantalla
es el 1. ¿Cuántas veces se debe apretar la tecla
"F" para obtener en la pantalla el número
1997?
ACLARACIÓN:
Si n es impar, d(n)=n.
23/8/97
Segundo día
4. Si n
> 1 es un número entero coprimo con 1997,
consideramos el conjunto An
formado por todos los números
i + ni/1997
, con i = 1, 2, 3, ...
, 1996
y todos los números
j + 1997j/n
, con j = 1, 2, 3, ...
, n-1
El conjunto An
tiene 1995+n números.
Ordenamos los números de An
en forma creciente:
a1![]() a
a2![]() ...
... ![]() a
a1995+n
Demostrar que ak+1-ak
< 2 para todo k =
1, 2, ... , 1994 + n.
5. En
una mesa rectangular hay hojas de papel cuadradas e
idénticas entre si, puestas de cualquier manera pero con
sus lados paralelos a los bordes de la mesa (las hojas
pueden estar total o parcialmente superpuestas).
Demostrar que es posible clavar
alfileres de modo que todas las hojas queden pinchadas a
la mesa pero cada hoja esté pinchada por un solo
alfiler.
6. Sea
n>1 un número
entero. Consideramos las palabras
de 2n letras,
compuestas por n
letras A y n letras B.
Una palabra X1X2.....X2n
se dice despareja si
ningún segmento inicial X1....Xk
(1![]() k < 2n)
tiene igual número de letras A que de letras B.
k < 2n)
tiene igual número de letras A que de letras B.
Una palabra X1X2.....X2n
se dice pareja si hay
exactamente un segmento inicial X1....Xk
(1![]() k < 2n)
que tiene igual número de letras A que de letras B.
k < 2n)
que tiene igual número de letras A que de letras B.
Si d(n)
es la cantidad de palabras desparejas y p(n)
es la cantidad de palabras parejas, calcular
p(n)/d(n)
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |