Costa Rica, 1996.

1. Sea n un número natural. Un cubo de arista n puede ser dividido en 1996 cubos cuyas aristas son también números naturales. Determine el menor valor posible de n.

2. Sea M el punto medio de la mediana AD del triángulo ABC (D pertenece al lado BC). La recta BM corta al lado AC en el punto N. Demuestre que AB es tangente a la circunferencia circunscrita al triángulo NBC si, y solamente si, se verifica la igualdad

3. Tenemos un tablero cuadriculado de k2-k+1 filas y k2-k+1 columnas, donde k=p+1 y p es un número primo. Para cada primo p, de un método para distribuir números 0 y 1, un número en cada casilla del tablero, de modo que en cada fila haya exactamente k números 0 y además no haya ningún rectángulo de lados paralelos a los lados del tablero con números 0 en sus cuatro vértices.

4. Dado un número natural n2, considere todas las fracciones de la forma 1/ab , donde a y b son números naturales, primos entre sí y tales que

a < b n

a + b > n

Demuestre que para cada n la suma de estas fracciones es 1/2.

5. Tres fichas A, B y C están situadas una en cada vértice de un triángulo equilátero de lado n. Se ha dividido el triángulo en triangulitos equiláteros de lado 1, tal como muestra la figura en el caso n=3.

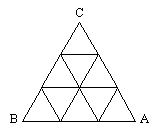
Inicialmente todas las líneas de la figura están pintadas de azul. Las fichas se desplazan por las líneas, pintando de rojo su trayectoria, de acuerdo con las dos reglas siguientes:

i. Primero se mueve A, después B, después C, después A y así sucesivamente por turnos. En cada turno cada ficha recorre exactamente un lado de un triángulo de un extremo a otro.

ii. Ninguna ficha puede recorrer un lado de un triangulito que ya esté pintado de rojo; pero puede descansar en un extremo pintado, incluso si ya hay otra ficha esperando allí su truno.

Demuestre qye oara todo entero n>0 es posible pintar de rojo todos los lados de los triangulitos.

6. Se tienen n puntos distintos A1 , ... , An en el plano y a cada punto Ai se ha asignado un número real distinto de cero, de manera que

para todos los i, j con ij.

Demuestre que

a) n 4

b) Si n=4, entonces

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar