Encontrar N y M enteros positivos, tales que los primeros tres decimales de (1/N)+(1/M) sean iguales a 236. O sea (1/N)+(1/M) = 0,236...

Hallar X,Y,Z enteros positivos que verifiquen simultáneamente las igualdades

X² + Y² = Z²

28·X + 10·Y + 2015·Z = 448103

Nicolás quiere escribir en el pizarrón una secuencia de 7 enteros positivos distintos, que empiece por 125 y termine en 2015, ordenada de menor a mayor de izquierda a derecha, para transmitirle un mensaje a María, su amiga otaku. Nicolás sabe que cuando María vea los números ella va a escribir debajo una nueva secuencia (ahora de 6 enteros, no necesariamente positivos ni distintos ni ordenados) donde cada número es la resta (en orden) de los dos números de arriba, como en el dibujo. Luego va a repetir el proceso varias veces, hasta que le quede una secuencia de 4 números. Nicolás quiere que en ese paso queden los números 83, 85, 75 y 73, en ese orden.

A=125

B

C

D

E

F

G=2015

B−A

C−B

D−C

E−D

F−E

G−F

???

???

???

???

???

83

85

75

73

a) ¿Qué números debería elegir Nicolás?

b) ¿Cuántas posibilidades tiene?

Hallar todos los X enteros tales que

X⁵ − 49·X⁴ + 624·X³ − 2064·X² + 623·X − 2015 = 0

En la fiesta de Mónica se van a repartir chocolatines (menos de 3000) entre los asistentes, al menos uno para cada uno, y la misma cantidad para todos. Si repartieran al comenzar la fiesta sobrarían 16 chocolatines. Al promediar la fiesta llegan 7 amigos más, entonces sobrarían 15 chocolatines. Ya casi terminando, como 4 amigos se han marchado sobran 24 chocolatines.

a) ¿Cuántos amigos de Mónica había al comienzo?

b) Si los invitados se van yendo de a uno, justo después de que lleguen los 7 amigos, ¿en qué punto convendría repartir para que sobre la mayor cantidad de chocolatines?

a) Hallar dos enteros positivos A y B, ambos de 4 cifras, de forma que A tenga 16 divisores, B tenga 8 divisores, A+1 tenga 4 divisores, B+1 tenga 36 divisores, A+B tenga 6 divisores, y que al concatenar A seguido de B quede un número de 8 cifras con 24 divisores. Por ejemplo al concatenar 1114 seguido de 7667 queda 11147667.

b) Hallar todas las posibles parejas de A y B que cumplen lo anterior.

a) Hallar X,Y,Z enteros positivos que verifiquen simultáneamente las igualdades

X² + Y² + Z² = 4061109

30·X + 10·Y + 2015·Z = 4061165

b) Hallar todas las soluciones posibles para el ítem a)

La siguiente tabla muestra los enteros positivos en la fila de arriba, y la cantidad de divisores correspondientes a cada uno en la fila de abajo:

Se va llenando por columnas, hasta que la fila de arriba contiene al número M.

a) ¿Cuál número tarda más en aparecer en la fila de abajo, si M = 2015?

b) ¿Cuál es el menor entero positivo que no aparece en la fila de abajo, si M = 2015?

c) ¿Cuál número tarda más en aparecer en la fila de abajo, si M = 4000000?

d) ¿Cuál es el menor entero positivo que no aparece en la fila de abajo, si M = 4000000?

Encontrar cuántas ternas de enteros positivos (A,B,C) existen tales que B es cuadrado perfecto, C es cubo perfecto, A+B = 2·(B+C), y A+C es múltiplo de 2015, cuando:

a) A,B,C < 10³          b) A,B,C < 10⁶          c) A,B,C < 10⁹

Aclaración: un número es cuadrado (cubo) perfecto si es el cuadrado (cubo) de algún entero. Por ejemplo 1, 4, 144 son cuadrados perfectos, y 1, 8, 125 son cubos perfectos.

Hallar todos los enteros positivos menores a 1000000 que no se pueden escribir como suma de un primo más un semiprimo. Un semiprimo es el producto de 2 primos (no necesariamente distintos). Por ej. 2015 = 1993 + 2·11, con 2, 11 y 1993 números primos.

Nota: Los primos son los números enteros mayores que 1 que sólo pueden dividirse por 1 y por si mismos: 2, 3, 5, 7, 11, 13, 17, 19, …

La Exposición Nacional del Alfajor inaugura el 1 de noviembre presentando un Alfajor Cuadrado Gigante. Cada día se hace una demostración de corte: el día de la inauguración lo cortan en 2 o 4 porciones, que se guardan en heladera. Luego cada día se sacan las porciones, algunas se cortan en 4 porciones y el resto en 2 porciones, y se vuelve a guardar todo en heladera. El 15 de noviembre, después de la demostración de corte se hace una degustación y se regalan las 510002 porciones. Dar una posible forma en que se hicieron los cortes (cuántas porciones se cortan en 4 el día 1, cuántas el día 2, etc.).

Llamaremos reflector a todo entero positivo R > 1 tal que existe N entero positivo que cumple que N·R es el reverso de N. En ese caso diremos que N es reflejable por R. El reverso de un número es el que se obtiene al dar vuelta sus cifras; por ejemplo el reverso de 2015 es 5102.

a) Hallar un ejemplo de reflector.

b) Dar todos los N y R, con N < 1000000, tales que R es reflector y N es reflejable por R.

c) Dar un R reflector y conjunto infinito de N reflejables por ese mismo R.

d) Demostrar que si R es reflector entonces es uno de los encontrados en b).

Sugerencia: usar la computadora para explorar.

a) Hallar dos parejas (A,B) distintas, con A y B enteros positivos y A ≤ B, que verifiquen

2015 < (A+B)^A+B − A^A·B^B < 20150

b) Hallar A y B enteros positivos y A ≤ B, que verifiquen

(A+B)^A+B − A^A·B^B = 816631

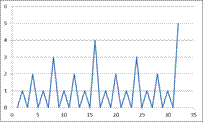
Agustín hace un gráfico de la siguiente función:
f(n) = exponente de la mayor potencia de 2 que divide a n.

Por ejemplo f(3) = 0, f(2) = 1, f(48) = 4, etc.

El gráfico de Agustín es la poligonal que une los puntos (1,f(1)), (2,f(2)), (3,f(3)), ..., (2015, f(2015)).

a) ¿Qué longitud tiene la poligonal?

b) ¿Qué longitud tiene la poligonal si el gráfico sigue hasta (2015², f(2015²)) ?

c) ¿Qué longitud tiene la poligonal si el gráfico sigue hasta (2015⁴, f(2015⁴)) ?

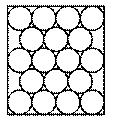Ramón tiene envases vacíos de gaseosas de cuatro marcas distintas, que llamaremos A, B, C y D. Los mete apretaditos en una caja, necesariamente como en la figura. Tiene 5 envases de A, 5 de B, 4 de C y 4 de D. Por su manía de ordenar no le gusta ver dos envases de la misma marca pegados (vecinos, en contacto).

a) ¿Tiene manera de acomodarlas?

b) ¿De cuántas maneras puede hacerlo?

Un entero positivo N tiene la propiedad de dividirse primalmente si existen enteros positivos A y B tales que A·B = N, A es primo y A+B también es primo. Encontrar cuántos enteros positivos menores a M NO cumplen la propiedad si...

a) M = 1000                                            b) M = 100000                                        c) M = 10000000

De todos los cuadrados perfectos menores que 10⁹, ¿cuál (o cuáles si hay más de uno) se puede escribir como suma de la mayor cantidad posible de cuadrados perfectos positivos consecutivos?

Aclaración: 36, 81, 121, etc. son ejemplos de cuadrados perfectos; 25, 36, 49 son tres cuadrados perfectos consecutivos; 18² + 19² + ... + 28² = 5929 = 77² es un cuadrado perfecto que es suma de 11 cuadrados perfectos consecutivos.

Nota: Tener cuidado con el overflow en las cuentas intermedias.

Sea s(N) la suma de los divisores de N, con N entero positivo. Por ejemplo s(1) = 1, s(2) = 3,

s(6) = 12. Diremos que N₁, N₂, ..., N_k forman una cadena (de longitud k, terminada en N_k) si son k enteros positivos tales que N₁ < N₂ < ... < N_k y además s(N₁) divide a s(N₂), s(N₂) divide a s(N₃), etc. Por ejemplo 1, 2, 6 es una cadena (de longitud 3, terminada en 6), porque s(1) divide a s(2), y s(2) divide a s(6).

a) Hallar una cadena de longitud 7.

b) ¿Cuál es la máxima longitud posible de una cadena de enteros positivos menores que 2015?

c) ¿Cuál es la máxima longitud posible de una cadena de enteros positivos menores que 1606061?

En b) y c) dar también en qué número termina una cadena de longitud máxima.