a) Hallar la cantidad de ternas de enteros positivos A,B,C tales que
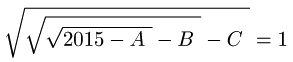
b) Hallar la cantidad de ternas de enteros positivos A,B,C tales que
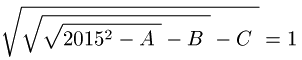
14 de agosto de 2015
Encontrar dos enteros positivos X, Y que cumplan que 4·X + 3·X·Y + 2·Y 2 = 16637442
Contar cuántas ternas de dígitos A,B,C todos distintos y no nulos cumplen que AB·BC es divisible por AC.
Ejemplo: 7,2,5 es una terna que cumple lo pedido.
Aclaración: AB es el número de 2 dígitos que tiene A en las decenas y B en las unidades, y análogamente para BC y AC.
Una máquina puede fabricar tres tipos de valijas (o maletas). Para la valija pequeña necesita 19 remaches, para la valija mediana necesita 26 remaches, y para la valija grande necesita 31 remaches. Para funcionar, la máquina es alimentada con cajitas de remaches que contienen 144 remaches cada una. Si se fabricaron 24 valijas y no se desperdició ni sobró ningún remache, ¿cuántas valijas de cada tipo se fabricaron? Dar todas las posibilidades.
Discutí tus soluciones de Nivel 1 en el Consultorio-CyM
Encontrar dígitos A, B y C tales que el producto 4A · 9B · 2C termine en 492.
Aclaraciones: 4A es el número de 2 dígitos que tiene 4 en las decenas y A en las unidades, y análogamente para 9B y 2C. 2015 termina en 15.
Julio extiende (hasta el 2015) el trazado usual de la rayuela así: todos los múltiplos de 4 van en casillas dobles, junto con el número anterior o el número posterior, eligiendo de entre ellos el que deja menor resto en su división por 5. Le queda como en este dibujo:
| 4 | 7 | 11 | 15 | 20 | |||||||||||||
| 1 | 2 | 3 | 6 | 9 | 10 | 13 | 14 | 17 | 18 | 19 | 22 | ... | |||||
| 5 | 8 | 12 | 16 | 21 | |||||||||||||
Para jugar, se da 1 salto para avanzar de casilla, pero con dos pies en las casillas dobles. Por ejemplo, hace falta 1 salto para llegar al 1, 3 saltos para llegar al 3, 4 saltos para llegar al 4 y al 5 (ya que se llega a ambos al mismo tiempo), 7 para llegar al 9, 12 para llegar al 15 y al 16, etc. ¿Cuántos saltos hacen falta para llegar al 2015?
a) Hallar tres enteros positivos X, Y, Z todos menores que 10000 que cumplan las siguientes dos ecuaciones simultáneamente:
2·X + 3·Y2 + 5·Z2 = 18143426
5·X + 4·Y2 + 2·Z2 = 10278149
b) Hallar todas las soluciones del ítem a.
Discutí tus soluciones de Nivel 2 en el Consultorio-CyM
a) Hallar valores para los dígitos (todos distintos) A, B, C, D, E y F de forma que los números de tres cifras ABC, DEF, CBA y FED cumplan
| ABC | = | CBA |
| DEF | FED |
b) Hallar todas las posibilidades.
Encontrar un entero positivo N tal que la suma de sus divisores sea divisible por 2015.
Ejemplo: Los divisores de 12 son 1, 2, 3, 4, 6 y 12, y la suma de los divisores de 12 es 28.
a) Hallar la cantidad de ternas de enteros positivos A,B,C tales que
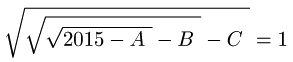
b) Hallar la cantidad de ternas de enteros positivos A,B,C tales que
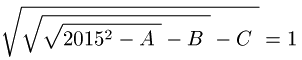
Discutí tus soluciones de Nivel 3 en el Consultorio-CyM