(A3+B3)-C3
1 y 1
(A3+B3)/C3
1,00001
Buenos Aires, 17 al 19 de octubre de 2012
|
|
Encontrar tres números enteros positivos A, B, C, todos distintos, tales que
0
(A3+B3)-C3
1 y 1
(A3+B3)/C3
1,00001
Beba y Gisel eligen cada una un número entero positivo. Si multiplican ambos números obtienen 65404922. Si Beba hubiera elegido el número anterior al que eligió y Gisel el siguiente al que eligió, al multiplicarlos hubieran obtenido 65396240. ¿Qué número eligió cada una? ¿Es la única posibilidad?
Encontrar todos los números de 7 cifras, de las cuales hay 6 que son iguales, que son múltiplos de 123.
¿Cuál es el mayor valor que puede tomar X•Y•Z
si X, Y, Z son enteros positivos tales que X2+Y2+Z210000?
Lucas considera los números enteros entre 2012 y 12012 ...
a) Encontrar todos los que tienen exactamente 21 divisores.
b) ¿Cuántos tienen por lo menos 20 divisores?
c) ¿Cuál o cuáles tienen la máxima cantidad de divisores?
¿Cuántos números de cuatro cifras ABCD hay tales que el resultado de multiplicar ABCD•DCBA es capicúa?
Nota: El número 12233221 es capicúa, pero 233320 no lo es.
Discutí tus soluciones de Nivel 1 en el Consultorio-CyM
Encontrar tres números enteros positivos X,
Y, Z tales que entre el mayor y el menor de ellos la diferencia
no es mayor que 5 y además X•2159 + Y•1779 + Z•1149 =
218630.
Tres tristes tigres tragan trigo de un trigal. Tristes están porque sólo trigo tragan. La primera tabla da el nombre de cada tigre, la cantidad mínima y máxima de kilocalorías que puede comer, y la cantidad mínima o máxima (en porcentaje del peso ingerido) que debe comer de cada macronutriente (proteínas, lípidos, hidratos de carbono).
| tigre | mín kcal | máx kcal | mín %prot. | mín %líp. | máx % hidr. carb. |
| Tristán | 6696 | 8184 | 18.5 % | 4.0 % | 70.0 % |
| Tirso | 5670 | 6930 | 16.5 % | 3.5 % | 75.0 % |
| Tatiana | 4653 | 5687 | 13.5 % | 3.0 % | 80.0 % |
Hay tres variedades de trigo. La segunda tabla da la composición nutricional de cada variedad, por cada pastilla de trigo de 100g que no se puede fraccionar, y cuántas pastillas disponibles hay.
| trigo | kcal | proteínas | lípidos | hidr. carb. | past. disponibles |
| germen | 360 | 23.15 | 9.72 | 51.80 | 18 |
| salvado | 216 | 15.55 | 4.25 | 64.51 | 22 |
| harinero | 331 | 10.35 | 1.56 | 74.24 | 30 |
a) Dar un menú posible, es decir, cuántas pastillas de cada variedad darle a cada tigre.
b) Dar todos los menús posibles.
Consideramos las ternas de números enteros positivos (P; Q; R) tales que P, Q, R y P2+Q2+R2 sean primos.
a) Encontrar 9 de ellas.
b) ¿Cuántas de ellas hay tales que P, Q, R son menores que 10000?
¿Cuántas ternas de números enteros positivos (X, Y, Z), todos menores que 1000, hay tales que X2+Y2+Z2 es un número que termina en por lo menos seis ceros?
Gastón escribe para cada número N entero positivo la tira de números 13+N, 23+N, 33+N, 43+N, 53+N, 63+N, ..., 10003+N.
Encontrar los 10 valores más chicos de N para los cuales su correspondiente tira no tiene ningún número primo.
Encontrar todos los números N de cuatro cifras, tales que de las cifras que aparecen en N2 no haya ninguna que no aparece en N.
Discutí tus soluciones de Nivel 2 en el Consultorio-CyM
Decimos que dos primos pertenecen a la misma familia si tienen exactamente los mismos dígitos permutados. Por ejemplo 137 y 317 pertenecen a la misma familia, en cambio 113 y 331 no pertenecen a la misma familia.
Considerando números de 6 dígitos, ¿cuántos integrantes tiene la familia más numerosa?
Demostrar que hay exactamente 13 números positivos de 8 cifras de la forma
X3 + Y3 - 100•X•Y
cuyas primeras cuatro cifras son 2012, con X e Y enteros positivos.
Nota: Por ejemplo, las primeras cuatro cifras de 201271021 son 2012.
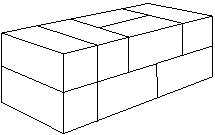a)
¿De cuántas formas es posible, con ladrillos de 2x1x1, construir una pared
maciza de 10x2x2?
b) ¿Y una pared maciza de 16x2x2?
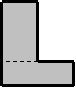Ariel
forma una L usando dos rectángulos de lados enteros, como se ve en la
figura. (El rectángulo de abajo es más ancho, para que la figura tenga la
forma correcta.) ¿Cuál es el mínimo perímetro exterior que puede conseguir
si la superficie de la L es 2012?
Dado un número racional a con 0<a<1, definimos
f(a) := 1/a - [1/a]
en donde [x] es la parte entera de x, o sea el máximo entero menor o igual que x.
A partir de un a se calcula: a, f(a), f(f(a)), f(f(f(a))), ...
Definimos el orden de a como la cantidad de veces que se debe aplicar f hasta obtener 0.
Por ejemplo f(1/3)=0, f(3/4)=1/3, f(f(f(4/11)))=f(f(3/4))=f(1/3)=0, por lo que orden(1/3)=1, orden(3/4)=2 y orden(4/11)=3.
De los números racionales p/q con 0<p<q<11000, ¿cuáles tienen orden máximo? ¿Cuánto es dicho orden?
a) Hallar números enteros positivos X, Y, Z tales que X2+Y2+Z2 termina en por lo menos cuatro cuatros.
b) ¿Cuál es la mayor cantidad de cuatros en la que puede terminar un número de la forma X2+Y2+Z2 con X, Y, Z enteros positivos?
Discutí tus soluciones de Nivel 3 en el Consultorio-CyM
 Archivo de Enunciados
CyM
Página
Principal
|
Olimpíada Matemática
Argentina www.oma.org.ar | info@oma.org.ar |
| mensajes webmaster@oma.org.ar |