Buenos Aires, 3 al 5 de octubre de 2011
|
|
Encontrar todas las cuaternas X, Y, Z, W de números enteros positivos tales que
X∙Y + Z∙W = 197
X∙Z + Y∙W = 203
Encontrar un número entero positivo X tal que 2011∙X2 + 10∙X + 1 sea primo.
a) Encontrar un número entero positivo X de 4 cifras que empiece en 23, que sea múltiplo de 13 y la suma de sus cifras sea 13.
b) Encontrar un número entero positivo Y de 4 cifras que empiece en 23, tal que Y2 sea múltiplo de 49 y la suma de las cifras de Y2 sea 49.
Un número entero positivo es casiprimo si es igual al producto de dos números primos distintos. Por ejemplo 6, 21, 65, 202 son casiprimos, pero los números 1, 2, 9, 12, 30, 125 no son casiprimos.
a) Entre 1998 y 2011, ¿qué años tienen número casiprimo?
b) ¿Cuál es el próximo año casiprimo?
a) ¿Cuántas ternas de enteros positivos X, Y, Z cumplen 1007∙X + 103∙Y2 + 23∙Z3 = 220011?
b) ¿Cuántas ternas de enteros positivos X, Y, Z cumplen 1007∙X + 103∙Y2 + 23∙Z3 = 22200011?
Teo tiene en su pantalla inicialmente el número 2011. Cada segundo, el número que aparece se cambia, de manera que si estaba el número X, aparece el número 3∙X + 1.
a) ¿En algún momento vuelve a aparecer un número terminado en “011”?
b) ¿En algún momento aparece un número terminado en “111”?
Discutí tus soluciones de Nivel 1 en el Consultorio-CyM
El luchador de sumo Konishiki llegó a pesar 287.0 kg.
a) ¿Cuáles 3 de los siguientes deportistas distintos tienen el peso combinado más cercano al peso de Konishiki?
| Aymar: 58.2 Conte: 89.5 Contepomi: 102.6 Corleto: 84.4 Curuchet: 71.3 Del Potro: 82.3 |
F. Lobbe: 109.4 Ginóbili: 92.5 Hernández: 92.7 Meolans: 87.4 Messi: 66.4 Milinkovic: 99.5 |
Nalbandian: 79.5 Oberto: 110.8 Palermo: 82.5 Pareto: 47.4 Pérez: 74.5 Pichot: 77.1 |
Prigioni: 89.7 Sabatini: 58.3 Scola: 111.0 Tévez: 70.9 Wolkowyski: 124.6 (suman 1962.5) |
b) Con 4 deportistas distintos.
En un tablero de 100x100, se coloca en la casilla de la fila X y columna Y el número X2 + Y. Las filas y columnas se numeran de 1 a 100.
a) Si S es la suma de los números escritos en el tablero, calcular la cantidad de ceros en que termina S. (Por ejemplo 1209000 termina en tres ceros.)
b) Si P es el producto de los números escritos en el tablero, calcular la cantidad de ceros en que termina P.
Se eligen cinco cifras no nulas A, B, C, D, E. Primero se forma el número de tres cifras X con las cifras A, B, C en algún orden. Luego se forma el número Y con las cifras C, D, E en algún orden. Finalmente forma el número Z usando las cinco cifras A, B, C, D, E en algún orden. Si X∙Y∙Z = 1050138888, encontrar cuánto valen X, Y y Z.
a) Entre todos los números de 6 cifras, formados por "2" y "8", ¿cuál es el que tiene más divisores? b) Entre todos los números de 8 cifras, formados por "2" y "8", ¿cuál es el que tiene más divisores?
Alejo el biólogo tiene un cultivo de bacterias. Si un día no aplica antibiótico, al día siguiente hay 20% más bacterias, redondeando hacia arriba. Por ejemplo de 136 pasa a 164, de 370 a 444, de 739 a 887, etc. En cambio, si un día aplica antibiótico, entre ese día y el siguiente muere el 10% de las bacterias, redondeando hacia abajo. Por ejemplo de 136 pasa a 123, de 370 a 333, de 735 a 662, etc.
El día 1 había una bacteria. ¿Cuál es la menor cantidad de bacterias que puede haber el día número 100? ¿Cómo se debe aplicar el antibiótico para lograrlo? (Dar alguna opción.)
a) Si por razones de salubridad, sólo se puede usar el antibiótico hasta 4 veces.
b) Si por razones de salubridad, sólo se puede usar el antibiótico hasta 10 veces.
Se ordenan alfabéticamente todas las permutaciones de 'secundario'. Así, 'acdeinorsu' ocupa el primer lugar, 'acdeinorus' el segundo, 'acdeinosru' el lugar 3, etc.
a) ¿En qué lugar queda 'secundario'?
b) ¿Cuál queda en el lugar 1284649?
Discutí tus soluciones de Nivel 2 en el Consultorio-CyM
a) Hallar un entero positivo X tal que 3 + 10∙X + 2011∙X2 − X3 es positivo y primo?
b) ¿Cuántos números enteros positivos X hay tales que 3 + 10∙X + 2011∙X2 − X3 es positivo y primo?
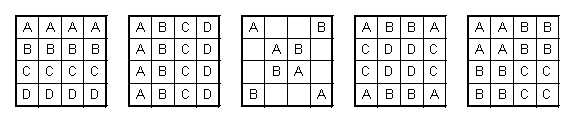
Un cuadrado mágico de Durero es una distribución de los números del 1 al 16 en un tablero de 4x4 de modo tal que cada fila, cada columna, cada una de las dos diagonales, las cuatro casillas del centro, las cuatro casillas de las esquinas, los dos "bordes" (ver figura) y cada uno de los cuatro cuadrantes sumen lo mismo.
a) Hallar un cuadrado mágico de Durero.
b) ¿Cuántos cuadrados mágicos de Durero hay? (Rotar o espejar da distinto cuadrado.)
Si
es un número real positivo, sea
f() la única solución
positiva de la ecuación tan(x) = (1+)∙x. Encontrar números reales
C y D
tales que para todo
en 1/10000, 2/10000, ... , 99/10000, 100/10000, el
valor absoluto de la diferencia entre C∙D y f() sea menor a 0,0015.
(Aclaración: en la ecuación, x está en radianes.)
a) ¿De cuántas formas se puede escribir 20112 como suma de cuatro cuadrados?
b) ¿De cuántas formas se puede escribir 20112 como suma de cuadrados? Por ejemplo 5 se puede escribir de dos formas, ya que 5 = 22 + 12 = 12 + 12 + 12 + 12 + 12.
a) De los números enteros entre 1 y 1000000, buscar alguno que tenga la mayor cantidad de divisores.
b) De los números enteros entre 1 y 1000000, buscar todos los que tengan la mayor cantidad de divisores.
c) De los números enteros entre 1 y 1000000000, buscar alguno que tenga la mayor cantidad de divisores.
d) De los números enteros entre 1 y 1000000000, buscar todos los que tengan la mayor cantidad de divisores.
Ariel quiere recortar un círculo de radio 1 en ocho piezas de
igual superficie realizando un corte recto que pasa por el centro, y otros
tres cortes perpendiculares al anterior como se ve en la figura. ¿Qué
distancias debe dejar entre los cortes paralelos? Aproximar estas distancias
con un error menor a 0,001.
Discutí tus soluciones de Nivel 3 en el Consultorio-CyM
 Archivo de Enunciados
CyM
Página
Principal
|
Olimpíada Matemática
Argentina www.oma.org.ar | info@oma.org.ar |
| mensajes webmaster@oma.org.ar |