Y tales que si se suman todos los números que son divisores de
X ó de Y
(ó de ambos) se obtiene 6721.
Buenos Aires, 15 al 17 de noviembre de 2010
|
|
a) Encontrar tres números enteros X, Y, Z todos mayores que 30 tales que X2 + Y2 + Z2 = 22739
b) ¿Cuántas ternas de números X, Y, Z de este tipo hay en total?
Encontrar un número de cinco cifras ABCBA primo, en dónde A, B, C son cifras y C = 3 ∙ A.
Enzo es muy supersticioso y quiere comprar exactamente 777 galletitas por $7,77. En el supermercado hay paquetes de 84 galletitas a $0,44; paquetes de 59 galletitas a $0,69; paquetes de 81 galletitas a $0,40 y paquetes de 45 galletitas a $0,67. ¿Puede comprar las galletitas que quería al precio que quería? ¿Tiene más de una opción? ¿Cuántos paquetes debería comprar en total en cada caso?
Alejo calcula todos los números de la forma 4 ∙ A ∙ B + A - 5 ∙ B en donde A y B son enteros mayores o iguales que 2010. Encontrar el menor de ellos que es primo.
Dado el número N, llamamos s(N) a la suma de las cifras de N. Por ejemplo si N = 1447 entonces s(1447) = 16.
a) Encontrar un entero positivo N tal que s(N) + s(N2) = 87.
b) Encontrar un entero positivo N tal que s(N) + s(N2) = 96.
a) Encontrar dos números enteros positivos
X Y tales que si se suman todos los números que son divisores de
X ó de Y
(ó de ambos) se obtiene 6721.
b) ¿Cuántas parejas de números (X; Y) de este tipo hay?
Discutí tus soluciones de Nivel 1 en el Consultorio-CyM
Encontrar cuatro números enteros positivos A, B, C, D tales que 3861 ∙ A + 2600 ∙ B + 2070 ∙ C + 64350 ∙ D = 10362690
¿Cuántos divisores de 20092010 terminan en 127?
Nota: Un número termina en 127 cuando sus 3 últimas cifras decimales son 1, 2, 7 en ese orden. Por ejemplo 90127, pero no 5721, que termina en 721.
a) Encontrar cuatro números enteros positivos A, B, C, D tales que el producto de las seis sumas posibles de dos de ellos sea 68428800.
b) ¿Cuáles son todas las cuaternas de números A, B, C, D de este tipo?
Los números abacanados son los enteros positivos que no se pueden escribir como la suma de tres cuadrados perfectos. Por ejemplo 7 es abacanado, pero 8=22+22+02 no.
a) Encontrar un número abacanado mayor que 210.
b) ¿Cuántos números abacanados hay entre 210 y 2010?
Ariel descompone el número N como producto de enteros positivos mayores que 1 y suma estos factores. Calcular cuántos resultados distintos puede obtener...
a) si N = 20100.
b) si N = 39916800.
Dado un primo P, se define F(P) como la posición de P en la lista de los números primos. Por ejemplo, F(2) = 1, F(3) = 2, F(5) = 3 y F(17) = 7.
Luego, dado un número N construímos la lista de números N, F(N), F(F(N)),... hasta encontrar el primer valor de la lista que no sea primo. Por ejemplo, para N = 17 la lista es 17, 7, 4 y ahí termina, dado que 4 no es primo; para N = 16, la lista sólo tiene al 16. Definimos el orden de N como la longitud de esta lista. Por ejemplo, el orden de 17 es 3 y el orden de 16 es 1.
Calcular la suma de los órdenes de todos los números entre 1 y N inclusive:
a) Para N = 18799716
b) Para N = 201082010
Discutí tus soluciones de Nivel 2 en el Consultorio-CyM
Encontrar un número primo de 6 cifras ABCDEF, tal que los números BCDEFA, CDEFAB, DEFABC, EFABCD y FABCDE también sean primos de 6 cifras.
¿Cuántas soluciones tiene la ecuación A ∙ B =
C, con A, B, C enteros positivos tales que A B, los dígitos de A y
B
juntos son todos distintos y no nulos, y los dígitos de C son todos iguales?
Por ejemplo 273 ∙ 814 = 222222 es una solución válida, pero 72 ∙ 12345679 = 888888888 no lo es.
a) De entre todas las tiras de 15 dígitos ordenados de menor a mayor, ¿cuántas hay que sumen 125?
b) De entre todas las tiras de 30 dígitos ordenados de menor a mayor, ¿cuántas hay que sumen 250?
c) De entre todas las tiras de 45 dígitos ordenados de menor a mayor, ¿cuántas hay que sumen 375?
Nota: Por ejemplo "0 0 0 1 1 2 3 3 4 4 4 6 8 8 8" es una tira de 15 dígitos que suma 52.
Para su tarea de lengua, Lucas debe buscar palabras con 3 vocales seguidas. Para facilitar su búsqueda hizo un programa que toma una palabra, revisa todas las permutaciones de sus letras, y muestra por pantalla todas aquellas permutaciones que tengan 3 vocales seguidas (aunque no sean palabras), sin repetir. Por ejemplo, si ingresa "AGUA", el programa muestra 6 permutaciones: AUAG GAAU GAUA GUAA UAAG AAUG
a) ¿Cuántas permutaciones muestra el programa si Lucas ingresa "FACILES"?
b) ¿Cuántas permutaciones muestra el programa si Lucas ingresa "COMPLICACIONES"?
Dado el número entero positivo N se calcula la suma de los recíprocos de todos sus divisores. Por ejemplo si N = 10 se obtiene 1 + 1/2 + 1/5 + 1/10 = 9/5. Hallar todos los N < 108 tales que dicha suma es entera.
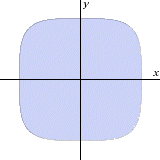Calcular el área del conjunto de puntos del
plano (X, Y) que verifican la inecuación X4 +
Y4
1.
a) Aproximar la respuesta con un error menor que 10-4.
b) Aproximar la respuesta con un error menor que 10-7.
c) Aproximar la respuesta con un error menor que 10-9.
Discutí tus soluciones de Nivel 3 en el Consultorio-CyM
 Archivo de Enunciados
CyM
Página
Principal
|
Olimpíada Matemática
Argentina www.oma.org.ar | info@oma.org.ar |
| mensajes webmaster@oma.org.ar |