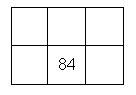
Rocío debe completar el tablero de 2x3 de la figura
con 5 números enteros positivos, uno en cada casilla libre (la del centro
abajo ya tiene 84), de manera que:
Buenos Aires, 18 al 20 de noviembre de 2009
|
|
Buscar todas las duplas de números enteros positivos X, Y tales que
(29 ∙ X + Y) ∙ (29 ∙ Y + X) = 28764800
Buscar un número primo de 6 cifras ABCDEF, tal que ABC sea un número de 3 cifras múltiplo de 7 y tal que DEF sea un número de 3 cifras múltiplo de 13.
Una exploración interplanetaria analizó varios animales. Estos animales tienen extremidades que pueden ser brazos, piernas, o colas, y de cada tipo pueden tener uno, varios o ninguno. Cualquier brazo tiene 32 huesos, cualquier pierna 30 huesos y cualquier cola 17 huesos. El análisis reveló que, contando sólo los huesos de extremidades, en total cada animal tiene la cantidad de huesos que indica la tabla.
| Animal | H | C | Z | P | X |
| Huesos | 124 | 1740 | 367 | 256 | 372 |
Además, se observó que H no tiene cola, C tiene menos brazos que los otros animales, Z tiene más colas que brazos y que piernas, y más colas que los otros animales, P no tiene piernas, y X tiene los tres tipos de extremidades. ¿Cuántas extremidades de cada tipo tiene cada animal? Dar todas las soluciones posibles.
Rocío debe completar el tablero de 2x3 de la figura
con 5 números enteros positivos, uno en cada casilla libre (la del centro
abajo ya tiene 84), de manera que:
¿Hay una única forma de llenarlo?
Se tienen dos tableros rectangulares (ambos con lados enteros), ambos con perímetro 198. Si en total tienen 4174 casillas, ¿cuánto mide cada uno?. Dar todas las soluciones.
Llamemos cerúleo a un número primo si es mayor a 100 y todas sus cifras son 0 salvo la primera y la última. Contar todos los primos cerúleos menores a 1000000000.
Buscar todas las soluciones de la ecuación
XA + YB = 454119265.
en las que X, Y, A, B sean todos enteros positivos mayores que 1.
Para armar un dado primo, se quieren 6 números primos P, Q, R, S, U, V que sean todos distintos y P+Q = R+S = U+V.
a) Encontrar P, Q, R, S, U, V que cumplan esta condición y que en total sumen por lo menos 1000.
b) ¿Cuáles se deben elegir para que se cumpla esa condición y la diferencia entre el mayor y el menor de los 6 números sea lo más chica posible? ¿Es la única elección posible?
La Tranquilísima tiene tres gustos de yogurt. El
yogurt de frutilla tiene 192 kilocalorías (kcal) y cuesta $2,27. El de
durazno tiene 184 kcal y cuesta $2,35. El de vainilla tiene 203 kcal y
cuesta $2,17. Durante los 31 días del mes se quiere comer un yogurt cada
día, de manera que no se coman dos del mismo gusto en días consecutivos y
que la cantidad de kilocalorías sea menor a 6000. ¿Cuál es el menor costo
posible?
Y para comer un yogurt por día durante 365 días sin repetir en días
consecutivos con menos de 71900 kcal ¿cuál es el menor costo posible?
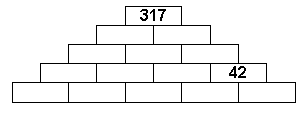Se tiene una pirámide formada por bloques
rectangulares. Cada bloque tiene un número entero positivo que es igual a la
suma de los dos de abajo. Además los números de la misma fila están
ordenados de menor a mayor (más chico a la izquierda).
Completar la pirámide con los números que faltan. ¿Cuántas formas de llenarla hay?
Encontrar un número primo ABCDEF de 6 cifras tal que los tres números de 2 cifras AB, CD, EF sean también todos primos.
En el país de "Las Mil y Una Noches" tres hermanos recibieron en herencia N camellos. Según el testamento, los camellos debían repartirse de la siguiente forma: 1/A de ellos para el hermano mayor, 1/B para el segundo y 1/C de los camellos para el hermano menor. Estaban perplejos, porque no se podía repartir de esa manera y que a cada uno de los tres hermanos le tocara una cantidad entera de camellos.
Lucas, un vecino, los salvó: les regaló 1 camello.
Entonces al repartir los N+1 camellos, a cada hermano le tocó ahora
una cantidad entera de camellos, y sobró 1 camello, que regalaron al vecino,
en agradecimiento.
Hallar todos los posibles valores de N, A, B, C
enteros positivos con A < B < C tales que se cumple
esta historia. Por ejemplo N=11, A=2, B=4, C=6.
a) Entre todos las duplas de números enteros X,
Y tales que –100
X100 y –100Y100, ¿cuántas verifican
que Y 
X2 ?
b) Ídem en –10000X10000 y –10000Y10000.
c) Ídem en –1000000X1000000 y –1000000Y1000000.
En un cuadrado de lado 1 se recortan de dos esquinas
opuestas sendos triángulos isósceles cuyos lados iguales miden L<1,
haciendo sendos cortes paralelos a la diagonal del cuadrado. La figura
resultante es un hexágono no regular H.
Aproximar con un error menor a 0,001 cuál debe ser L para que
Superficie(H)/Perímetro(H) sea máximo.
La función contadora de primos se define como
pi(N) = cantidad de números primos positivos menores o iguales que N.
Por ejemplo pi(1) = 0, pi(10) = 4, pi(100) = 25, pi(1000) = 168, pi(10000) = 1229.
a) Dar el valor exacto de pi(2009).
b) Dar el valor exacto de pi(123456789).
c) Dar el valor exacto de pi(1234567890).
Pista: notar que no se pide cuáles son los primos, solamente cuántos hay, menores o iguales que N.
Escribir X como suma de fracciones con numerador 1 y denominadores todos distintos, de manera que el mayor denominador utilizado sea lo más chico posible.
Por ejemplo: 1/2 + 1/4 +1/6 = 11/12, y 1/1 + 1/2 + 1/6 = 5/3.
a) X = 5/2
b) X = 547/220
La sucesión de Fibonacci se define de la siguiente manera:
Fib(1) = 1
Fib(2) = 1
Fib(N) = Fib(N–1) + Fib(N–2) cuando N>2
Por ejemplo Fib(3)=2, Fib(4)=3, Fib(5)=5, Fib(6)=8, Fib(6)=13, Fib(7)=21, …
a) Buscar el menor N tal que las últimas tres cifras de Fib(N) sean 747.
b) Buscar un número de tres cifras ABC tal que no existe ningún N para el cual las últimas tres cifras de Fib(N) sean ABC.
Esteban tiene una máquina con dos botones y un
indicador que inicialmente marca 1. Si toca el botón rojo, el número del
indicador aumenta en 100. Si toca el botón verde, el número del indicador
cambia por el primer primo mayor estrictamente que él.
Por ejemplo: 1(V) --> 2(V) --> 3(V) --> 5(R) --> 105(V) --> 107(R) --> 207.
Debe tocar 1000 veces el botón verde y 1000 veces el botón rojo, eligiendo
el orden en que los presiona. ¿Cuál es el máximo número al que se puede
llegar?
 Archivo de Enunciados
CyM
Página
Principal
|
Olimpíada Matemática
Argentina www.oma.org.ar | info@oma.org.ar |
| mensajes webmaster@oma.org.ar |