12do
Torneo de Computación
y Matemática
Certamen
Zonal
9 de octubre de 2009
Nivel 1(7mo y 8vo año de
escolaridad)
1
Buscar todas las cuaternas X, Y, Z,
R de números enteros positivos, todos menores que 20, tales que X2
+ Y2 + Z2 = R2, y tales que X, Y, Z
y R no tienen un divisor común (a todos) mayor a 1. Por ejemplo 6,
12, 9 y 18 tienen un divisor común, el 3, que es mayor a 1.
2
Encontrar un número D de seis cifras de la
forma D = 23??32, que no tenga ningún divisor entre 100 y 10000.
3
En un tablero rectangular (cuadriculado) se colocan 27
monedas en cada casilla de las esquinas, 23 monedas en cada casilla que toca
exactamente 1 borde del tablero y 17 monedas en las restantes casillas. Si
en total hay 14740 monedas, ¿de que tamaño es el tablero?
Nivel 2(9no y 10mo año
de escolaridad)
1
a) Buscar un X entero positivo tal que 3·X3
- 4018·X2 + 1020305·X + 229445566 < 0.
b) ¿Cuántos cumplen esta propiedad?
2
¿Cuántos triángulos rectángulos no congruentes tienen
área que divide a 20092009?
3
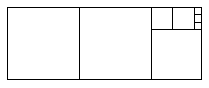Si
nos dan un rectángulo de lados A y B (con A > B
> 0, A y B enteros), lo llenamos con cuadrados de la siguiente
manera, por pasos: en el primer paso, llenamos con cuadrados de lado B,
sin superponerlos, sin espacio entre ellos, empezando desde el borde
izquierdo, hasta que ya no se puede más; en los siguientes pasos llenamos el
rectángulo que queda libre con cuadrados cuyo lado sea igual al lado más
chico del rectángulo, sin superponerlos, sin espacio entre ellos, empezando
desde el borde izquierdo o inferior según corresponda; como en la figura. El
proceso termina cuando llenamos todo el rectángulo AxB.
Para cada uno de los 10 rectángulos cuyos lados
(distintos) son 2 de estos números,
410105312, 150869313, 832040, 514229, 2009
hallar en cada caso:
- la cantidad de cuadrados usados para llenarlo según
el procedimiento anterior, y
- el lado del cuadrado más chico que se usó.
Nivel 3(11er año de escolaridad en
adelante)
1
Entre los números enteros positivos que son múltiplos
de 101 y menores que 1000000, encontrar los que tengan la mayor cantidad de
divisores.
2
Las ecuaciones A3 + B3
= C3 y A4 + B4 = C4
no tienen soluciones con A, B, C enteros positivos,
pero sí tienen solución con A, B, C, D, E
enteros positivos las ecuaciones
(i) A3 + B3 + C3
= D3
(ii) A4 + B4 +
C4 + D4 = E4
Hallar una solución de la ecuación (i) y una solución
de la ecuación (ii).
Nota: en (ii) las soluciones son tales que algunos
números intermedios son mayores a 232.
3
Si
nos dan un rectángulo de lados A y B (con A > B
> 0, A y B enteros), lo llenamos con cuadrados de la siguiente
manera, por pasos: en el primer paso, llenamos con cuadrados de lado B,
sin superponerlos, sin espacio entre ellos, empezando desde el borde
izquierdo, hasta que ya no se puede más; en los siguientes pasos llenamos el
rectángulo que queda libre con cuadrados cuyo lado sea igual al lado más
chico del rectángulo, sin superponerlos, sin espacio entre ellos, empezando
desde el borde izquierdo o inferior según corresponda; como en la figura. El
proceso termina cuando llenamos todo el rectángulo AxB. Hallar
A primo tal que cualquier rectángulo de AxB (A > B
> 0, A y B enteros) se cubre con igual o más cuadrados que el
rectángulo de Ax2009.
