11^er Torneo de Computación y Matemática

Certamen Nacional

Buenos Aires, 19 al 21 de noviembre de 2008

Web www.oma.org.ar

Nivel 1(7^mo y 8^vo año de escolaridad)

Primer día

1

Encontrar todas las ternas de enteros positivos X, Y, Z, todos estrictamente mayores que 1 y menores que 1000, tales que

X³ + Y³ = Z³ + 1.

2

Encontrar el menor entero positivo N tal que la suma de las cifras de N² es 28.

Nota: La suma de las cifras de 12472 es 1 + 2 + 4 + 7 + 2 = 16.

3

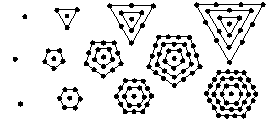
Los números poligonal-centrados, correspondientes a L lados y K pasos (L 3 y K 1), son las cantidades de puntos de figuras como las del dibujo.

Para todo L, el paso K = 1 es 1 punto. Para L lados y K > 1 pasos, la figura del paso K es como la figura del paso K−1 más un polígono de L lados con K puntos en cada lado (ver dibujo). Por ejemplo si L = 3 los números triangular-centrados son 1, 4, 10, 19, 31, 46, etc., si L = 5 los números pentagonal-centrados son 1, 6, 16, 31, 51, 76, etc., para K = 1, 2, 3, 4, 5, 6, etc.
Diremos que un número es poligonal-centrado no-trivial, o pocenotri, cuando es un número poligonal-centrado con L 3 y K 3. Por ejemplo 10, 19, 41, 127 son pocenotris.

Decir cuáles de los siguientes números son pocenotris y cuáles no. Para los que son pocenotris, dar además algún L y K con los que se obtiene dicho número.

2007, 2008, 2009, 4849846, 5837371, 48266900, 632718793

Segundo día

4

Encontrar todas las posibles ternas de números enteros positivos A, B y C tales que

(100∙A + 10∙B² + C³) = 218533

(100∙B + 10∙C² + A³) = 287737

(100∙C + 10∙A² + B³) = 185998

5

Encontrar todos los enteros positivos de 7 cifras que son divisibles por 7 y son cubos perfectos, pero que no son cuadrados perfectos.

Aclaración: un entero es cuadrado perfecto si es el cuadrado de otro entero, por ejemplo 1, 4, 9, 16, 25, etc.; y es cubo perfecto si es el cubo de otro entero, por ejemplo 1, 8, 27, 64, 125, etc.

6

Ariel quiere un número N de ocho cifras de la forma 33A55B77, en donde A y B son cifras, tal que N sea múltiplo de 123 y el número que se obtiene al dar vuelta N también es múltiplo de 123. ¿Hay algún número como el que busca Ariel? Si es así dar uno de ellos.
Nota: El número que se obtiene al dar vuelta 20081234 es 43218002.

Nivel 2(9^no y 10^mo año de escolaridad)

Primer día

1

a) Encontrar A, B, C, D enteros positivos tales que

A² + B³ + C⁴ + D⁵ = 55000

b) De todos los enteros entre 1 y 100000, buscar el mayor que no se puede escribir como A² + B³ + C⁴ + D⁵, con A, B, C, D enteros positivos.

2

¿Cuáles son todos los números de la forma AABBCC que tienen al menos 150 divisores?

Aclaración: Los divisores de 60 son 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 y 60.

3

Para cada F = 2, 3, 4, 5, 6, 7, 8, 9 hallar al menos una pareja de enteros positivos C y M tal que C/M = 1/F y además C y M juntos se escriben usando todos los dígitos 1, 2, 3, 4, 5, 6, 7, 8, 9 exactamente una vez.
Por ejemplo si F = 7, no sirve 63152/442064 porque usa el 0 y repite el 2, el 4 y el 6. Tampoco sirve 1863/27945 = 1/15 porque F no es como se pide.

Segundo día

4

Martín escribió todos los números K de 6 cifras tales que existe un entero positivo N tal que K divide a 2244^N. ¿Cuántos números escribió en total?

5

a) Encontrar 4 números primos de 2 cifras, tales que las 8 cifras que aparecen en total son todas distintas, y la suma de los 4 números es la menor posible.

b) Encontrar 3 números primos de 3 cifras, tales que las 9 cifras que aparecen en total son todas distintas, y la suma de los 3 números es la menor posible.

c) Encontrar 2 números primos de 4 cifras, tales que las 8 cifras que aparecen en total son todas distintas, y la suma de los 2 números es la menor posible.

6

Hallar todos los enteros positivos N tal que la suma de las cuartas potencias de las cifras de N sea igual a N.

Por ejemplo, la suma de las cuartas potencias de las cifras de 2008 es 16 + 0 + 0 + 4096 = 4112, así que 2008 no sirve.

Nivel 3(11^er año de escolaridad en adelante)

Primer día

1

Se consideran las siguientes 500 ecuaciones:

1∙A + B² + C² = 18081
2∙A + B² + C² = 18081
...
499∙A + B² + C² = 18081
500∙A + B² + C² = 18081

Encontrar una de ellas que no tenga ninguna solución en la que A, B y C sean números enteros positivos.

2

Dos primos de 5 cifras están conectados si uno puede obtenerse a partir del otro cambiando el valor de exactamente una cifra.

a) Decidir si se puede hacer una sucesión de primos de 5 cifras conectados así:

20089 --> A --> B --> C --> D --> 20107

Si no, buscar el camino más corto. En ambos casos dar los primos intermedios.

b) Decidir si se puede hacer una sucesión de primos de 5 cifras conectados así:

20089 --> A --> B --> C --> D --> 40087

Si no, buscar el camino más corto. En ambos casos dar los primos intermedios.

3

En un círculo de radio 1000 se dibuja un hexágono regular inscripto, de manera que tenga dos lados horizontales, y se marca el diámetro horizontal que divide ambas figuras a la mitad. Luego se pinta la parte superior del círculo y la parte inferior del hexágono.
Se quieren trazar dos rectas verticales, tales que la parte pintada quede dividida en tres partes de igual área. ¿A qué distancia deben estas las rectas verticales entre sí? Aproximar la solución con un error menor a 0,001.

Segundo día

4

Rodrigo escribió, ordenados de menor a mayor, todos los números racionales entre 0 y 1 (ambos inclusive) que se expresan como fracción irreducible con denominador menor o igual a 2008.

a) ¿Cuántos números escribió en total?

b) ¿Cuánto suman? Dar el valor exacto.

c) ¿Cuál ocupa el lugar 2008?

d) El 127/2008, ¿qué lugar ocupa?

Nota: el 0 ocupa el lugar 1, el 1/2008 ocupa el lugar 2, etc.

5

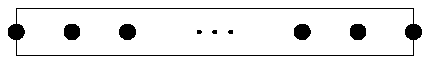A lo largo de un boulevard hay 34 faroles, ubicados como en la figura. Los faroles están separados 3 m entre sí. Cada uno puede iluminar un círculo de radio 8m con centro en el farol. El boulevard es rectangular, de 99 m de largo y 180 cm de ancho.

Una configuración (de encendido) es válida si se encienden exactamente 13 faroles y todo el boulevard queda iluminado. ¿Cuántas configuraciones válidas hay?

6

Consideremos la siguiente ecuación, con A, B y C enteros positivos:

A∙B∙C = A + B + C + 2008

a) Hallar todas las soluciones con A, B y C menores que 1000.

b) Hallar todas las soluciones.

Archivo de Enunciados CyM Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar