10^mo Torneo de Computación y Matemática

Certamen Nacional

Mar del Plata, 21 al 24 de noviembre de 2007

Web www.oma.org.ar

Nivel 1(7^mo y 8^vo año de escolaridad)

Primer día

1

Carolina eligió dos números enteros positivos A y B (ambos distintos de 0). Luego calculó C = B + A, D = C + B, E = D + C, F = E + D, G = F + E, H = G + F, I = H + G, J = I + H y K = J + I. Sorprendentemente al calcular K obtuvo 2007.

a) Encontrar algún posible valor de A y B que puede haber elegido.

b) ¿Es la única posibilidad?

2

a) Encontrar dos números primos positivos p y q tales que p - q = 7002.

b) ¿Cuántas parejas de números primos positivos p y q hay tales que p - q = 7002 y q 2007?

3

En una biblioteca se compraron tres colecciones de libros de manga. Todos los libros de cada colección tienen la misma cantidad de páginas. Los de la primera colección tienen 128 páginas, los de la segunda tienen 142 páginas y los restantes 164 páginas.

Si se cuentan las páginas de los libros de las dos primeras colecciones se tienen en total 2402. Si se cuentan las páginas de los libros de las dos últimas colecciones se tienen en total 1814.

¿Cuántas páginas tienen cada colección en total?

Segundo día

4

Hallar cifras distintas A, L, G, O, R, D, T, S, P, M tales que

ALGORS + DATAST = PROGRAM

Nota: ALGORS indica el número de seis cifras formado por las cifras A, L, G, O, R; DATAST indica el número de seis cifras formado por las cifras D, A, T, A, S, T; PROGRAM indica el número de siete cifras formado por las cifras P, R, O, G, R, A, M.

5

Encontrar dos números X e Y enteros mayores o iguales que 2 tales que

X^Y + Y^X = 94932

6

Se escriben en una hoja todos los números enteros positivos desde 1 (inclusive) hasta 1529910990 (inclusive). Hallar enteros positivos M y N tales que si recortamos de la hoja todos los múltiplos de M y todos los múltiplos de N, habremos recortado 20072007 números.

Nivel 2(9^no y 10^mo año de escolaridad)

Primer día

1

Encontrar dos números primos positivos p y q, ambos mayores que 2007, tales que q - p = 2 y además p + q + 1 también sea primo.

2

Calcular de cuántas formas se pueden elegir cinco números enteros A, B, C, D y E tales que

0 < A < B < C < D < E < 100

y

A - 0 25, B - A 25, C - B 25, D - C 25, E - D 25, 100 - E 25.

3

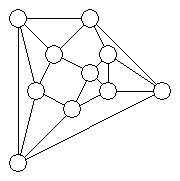
Nicolás quiere colorear todos los circulitos del siguiente dibujo de color rojo, azul, amarillo y verde, de manera que cada circulito tenga un solo color y los circulitos que están unidos directamente por un segmento de los marcados tengan colores diferentes.

a) Dar una posible forma en que se pueda colorear.

b) ¿Cuántas formas posibles hay en total?

Segundo día

4

Un pequeño club tiene tres divisiones: atletismo, básquet y ciclismo. Cada mes, los socios pagan $49 si pertenecen a una sola división, pero si pertenecen a dos pagan $40 a cada una, porque les hacen descuento. Por ahora nadie está anotado en las tres. La recaudación del mes pasado fue de $3831 en atletismo, $11756 en básquet, y $2007 en ciclismo. ¿Cuántos socios tiene cada división, y cuántos el club?

5

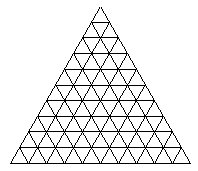
¿Cuántos triángulos equiláteros de cualquier tamaño y orientación hay dibujados en esta figura?

6

• Si el número es par, se lo reemplaza por su mitad.
• En cambio, si el número es impar se le suma 2007.

10 5 2012 1006 503 2510 ...

a) ¿Cuántos son los números que se pueden elegir como número inicial para que en algún momento vuelva a aparecer el número inicial?

b) ¿Cuáles son? (Describir el conjunto.)

Nivel 3(11^er año de escolaridad en adelante)

Primer día

1

Nicolás escribe todos los números enteros positivos en una lista, ordenados y empezando por el 1. Luego tacha todos los que tienen el dígito 9 al menos una vez. Después tacha todos los múltiplos de 3. Considerando solamente los números no tachados,

a) ¿qué número queda en la posición 100000?

b) ¿qué número queda en la posición 100000000?

2

Dado un número entero positivo n se calcula la suma de sus divisores y se la divide por n². Si el resultado es mayor a 0,01 entonces decimos que n es un número fluorescente.

a) ¿Cuántos números enteros positivos fluorescentes hay menores que 207?

b) ¿Cuántos números enteros positivos fluorescentes hay en total?

3

Hallar un número entero positivo M tal que 2007 · M = 999...999.

Nota: 999...999 indica un número cuyas cifras son todas 9.

Segundo día

4

¿De cuántas maneras se pueden poner nueve números desde 0 (inclusive) hasta 13 (inclusive), no necesariamente distintos, en un tablero de 3x3 sin que haya dos iguales en una misma fila o una misma columna?

5

Encontrar tres cifras no nulas A, B y C, todas distintas, tales que al escribir el resultado de AABBBCCC² aparezca escrito el número 2007.
Por ejemplo al escribir 462007892 aparece escrito el número 2007, pero no aparece escrito el número 6289.

Nota: AABBBCCC indica el número de ocho cifras formado por dos A, tres B y tres C.

6

Para todos los enteros positivos n consideramos las siguientes funciones:

s(n) = suma de los dígitos de 

p(n) = producto de los dígitos no nulos de n

f(n) = s(n)∙p(n)/n

Por ejemplo f(2007) = (2+0+0+7)∙(2∙7)/2007 = 9∙14/2007 ≈ 0,06278

a) Hallar el máximo valor de f(n), y dar un n donde f(n) valga eso, si n < 200000.

b) Hallar el máximo valor que puede tomar f(n), y dar un n donde f(n) valga eso.

Archivo de Enunciados CyM Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar