Mar del Plata, 20 al 23 de noviembre de 2006
|
|
Encontrar tres números enteros positivos X; Y; Z tales que
2 · X 2 + 6 · Y 2 + Z = 2006
y además X + Y + Z sea menor que 50.
Encontrar un número primo P > 0 tal que P + 1 sea múltiplo de 2006.
(Nota: Un número es primo si tiene exactamente dos divisores positivos distintos. Por ejemplo 2, 3, 5, 7, 11, 13, 17, 19, ... )
Para una fiesta de casamiento se compraron 7 botellas de $53, 11 botellas de $37 y 8 botellas de $66. Como los novios se pelearon, se suspendió la fiesta y decidieron repartir las botellas de manera que el precio total de cada una de las dos partes sea el mismo.
a) ¿Es posible repartirlas así?
b) ¿Es posible repartirlas de manera que, además del precio total, la cantidad de botellas sea igual?
Encontrar el número entero positivo más grande D tal que D 2 divide a 2052258360
Para cada uno de los siguientes valores de R, calcular la cantidad de pares (X;Y) tales que X e Y son números enteros y
(R - 1)2 ![]() X
2 + Y 2
X
2 + Y 2 ![]() (R
+ 1)2
(R
+ 1)2
cuando:
a) R = 100
b) R = 1000
c) R = 10000
Leandro eligió un número de 8 cifras que es capicúa, la suma de sus cifras es 26 y además es múltiplo de 35. Encontrar todos los números que puede haber elegido.
(Nota: Un número es capicúa cuando al invertir el orden de sus cifras se obtiene el mismo número. Por ejemplo 12344321, 11822811, 20066002, ...)
El 1 de noviembre de 2006 se compraron dos potes de 1Kg de helado, uno de vainilla y otro de chocolate.
Del helado de vainilla, el primer día comen 1/3 del pote. El segundo 1/5 de lo que queda. El tercero 1/7 de lo que queda. El cuarto 1/9 de lo que queda, y así sucesivamente.
Del helado de chocolate, el primer día comen 1/9 del pote. El segundo 1/25 de lo que queda. El tercero 1/49 de lo que queda. El cuarto 1/81 de lo que queda, y así sucesivamente.
Calcular cuánto helado queda de cada sabor después de comerlo durante:
a) 1 semana (7 porciones) b) 1 mes (30 porciones) c) 1 año (365 porciones)
Aproximar todos los resultados con un error menor que 0,000001.
Para generar un mensaje en clave se toma una palabra y cada letra se reemplaza por el número correspondiente a su orden alfabético: la A por un 1, la B por un 2, y así (sin tener en cuenta la "ñ", "ch", "ll" y "rr"). Por ejemplo: "PATO" -> 16, 1, 20, 15
Luego cada número se multiplica por una clave secreta K (un entero positivo) y se toman los últimos cuatro dígitos. Estos números que quedan forman el mensaje encriptado. Por ejemplo: Si K = 9990 entonces "PATO" en clave es 9840, 9990, 9800, 9850
Hemos interceptado un mensaje encriptado de esta manera y queremos descifrarlo. Dicho mensaje es: 864, 5679, 2222, 3580, 9259, 7654, 5679. Lamentablemente no sabemos cuál es la clave secreta K.
¿Cuál es la palabra original?
Todas las semanas, los mismos 12 clientes llaman a la empresa LAX para hacer sus pedidos. La empresa tiene suficientes líneas como para atender a todos al mismo tiempo, si es necesario, y nunca da ocupado. Los clientes eligen al azar uno de los 5 días hábiles de la semana y hacen su llamada. Se anota en una planilla semanal qué día llama cada cliente.
a) ¿Cuántas posibles planillas distintas hay en total?
b) ¿En cuántas planillas del item a) hay al menos un día hábil en que no llamó ningún cliente?
c) ¿En cuántas planillas del item a) hay exactamente un día hábil en que no llamó ningún cliente?
Encontrar un número de 10 cifras ABCDEFGHIJ tal que se cumplan simultáneamente las siguientes ocho condiciones
A principio de 2006 Javier plantó una semilla de jacarandá, de la que salió un tallo, que luego será el tronco. Todas las primaveras, en la punta del tronco y de cada rama sale una flor, redonda. Luego, en verano, cerca de cada flor salen algunas ramitas, que al año siguiente ya son ramas.


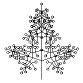
En las ramas nuevas, que tienen 1 año, salen 2 ramitas. En las que tienen 2 años salen 4 ramitas. En las que tienen 3 años salen 4 ramitas y en todas las otras salen 2 ramitas. En el tronco salen también 2, 4, 4, 2, 2, 2, 2, 2, ... ramas respectivamente según su edad, como muestra el diagrama.
Y así, salen nuevas ramas todos los años. En la primavera de 2015, ¿cuántas flores saldrán?
Se quiere alambrar una parte de un campo, encerrando una superficie de área 360m2, cuya forma es un trapecio rectangular donde la base mayor mide el doble que la base menor. Como muestra el dibujo, uno de los lados da a la ruta y hay que utilizar alambre reforzado que cuesta $5 el metro. En los otros tres lados se utiliza alambre normal que cuesta $2 el metro. Calcular los lados del trapecio que hacen que el precio sea mínimo si:
a) Los lados son enteros. (O sea, una cantidad entera de metros.)
b) Los lados son arbitrarios. Aproximar cada lado con un error menor que 0,001.

Es un hecho que para cualquier número de dos dígitos AB (con A>0), existe un número primo P cuya expresión decimal empieza AB... Por ejemplo si AB es 20, P podría ser 2003.
Se consideran todos los números primos mayores que 10, ordenados de menor a mayor. De todos los posibles pares de dígitos, ¿cuál es el último que aparece como el comienzo de un primo?
Luis creía que todos los números pueden ser expresados como suma de una o más potencias distintas de 4, 5 y 7 (cada potencia usada a lo sumo una vez). Por ejemplo:
1 = 4 0
2 = 4 0 + 5 0
3 = 4 0 + 5 0 + 7
0
4 = 4 1
5 = 4 1 + 4 0
6 = 4 1 + 4 0 + 5
0
7 = 4 1 + 4 0 + 5 0 +
7 0
8 = 4 0 + 7 1
...
76 = 4 2 + 4 1 + 7 1+
7 2
...
Sin embargo Brian se dio cuenta de que no es así. Hallar el número más chico que no se puede expresar de esta manera.
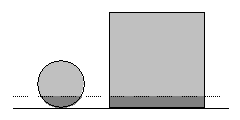
Sobre una recta horizontal se apoya un círculo de radio 1 y un cuadrado de lado 4. Luego se traza otra recta horizontal (distinta) que divide a cada figura en dos partes. Si se calcula el cociente entre la parte de arriba y la de debajo de cada figura, se obtiene el mismo valor en ambas.
Aproximar la distancia entre las dos rectas con un error menor a 0,001.
Una forma de generar números pseudo-aleatorios es la siguiente:
Xn+1 = (A · Xn + B) mod M
donde A; B; M son enteros tales que 0
![]() A; B; M, y además si K es
un número entero, K mod M es el resto de la
división entera de K dividido M.
A; B; M, y además si K es
un número entero, K mod M es el resto de la
división entera de K dividido M.
Por ejemplo si A = 3, B = 1, M = 10 y X0 = 5 entonces X1 = (3·5+1) mod 10 = 6, X2 = (3·6+1) mod 10 = 9, X3 = (3·9+1) mod 10 = 8, X4 = (3·8+1) mod 10 = 5, ...
Hallar, si existen, X0, A, B y M que den lugar a las siguientes secuencias:
a) X1 = 314, X2= 271, X3 = 206, X4= 130, ...
b) X1 = 3141, X2= 2717, X3 = 2006, X4= 1817, ...
c) X1 = 500, X2= 422, X3 = 283, X4= 422, ...
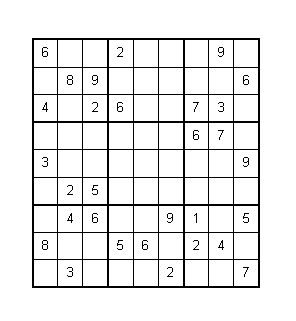
Se tiene un tablero de 9x9 dividido en 9 subtableritos de 3x3. En algunos de sus casilleros hay números como se ve en la figura. Llenarlo con números enteros del 1 al 9 de manera que en cada fila, en cada columna, en cada subtablerito no haya números repetidos.
Dado un número entero N llamamos S6(N) a la suma de la sexta potencia de sus cifras. Por ejemplo
S6(2) = 64
S6(2006) = 26 + 06 + 06 + 6 6 = 46720
a) Buscar un número A mayor que 10 tal que A = S6(A).
b) Buscar el número más grande B tal que B = S6(B).
|
|
Olimpíada Matemática
Argentina www.oma.org.ar | info@oma.org.ar |
| mensajes webmaster@oma.org.ar |