9^no Torneo de Computación y Matemática

Primera Ronda

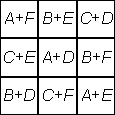
 25 de agosto de 2006

Web www.oma.org.ar

Nivel 1(7^mo y 8^vo año de escolaridad)

1

Encontrar tres números enteros positivos X; Y; Z, todos distintos, tales

646 · X + 2006 · Y = 39 · Z

2

Buscar un número entero positivo D mayor que 1, que sea divisor de 2070 y tal que además D+1 sea divisor de 2071.

3

En un parque de diversiones ganan $14.000 cada día soleado, pierden $9.000 cada día de lluvia y los días nublados no pierden ni ganan dinero. Si el mes pasado (julio de 2006) ganaron $226.000, ¿cuántos días nublados hubo ese mes?

Nivel 2(9^no y 10^mo año de escolaridad)

1

Se eligen seis números enteros no negativos A; B; C; D; E; F y con ellos se llena una tablero de 3x3 como se muestra a la izquierda. Al realizar las operaciones se obtiene el tablero de la derecha. Encontrar una posible elección de los seis números originales.

2

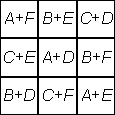
Encontrar tres dígitos X; Y; Z tales que

X · XY · Y · YZ · Z · ZX = 40544784

Nota: XY, YZ y ZX son números de dos cifras.

3

Se necesita comprar al menos 300 foquitos para un edificio nuevo. Se venden en paquetes grandes de 42 unidades y paquetes chicos de 34 unidades. El paquete grande cuesta $35 y el chico $31. Además se puede comprar medio paquete, pero con un recargo. El medio paquete grande cuesta $20 y el chico $18. ¿Cuánto es lo mínimo que se debe gastar?

Nivel 3(11^er año de escolaridad en adelante)

1

Se consideran todos los números de la forma 73 · A + 85 · B + 97 · C, en dónde A, B y C son números enteros positivos. ¿Cuál de ellos es el más cercano a 1000 por abajo, y cuál por arriba? 

2

¿De cuántas formas distintas se pueden elegir cuatro números enteros positivos A, B, C, D tales que son todos distintos entre sí y además A divide a B, B divide a C, C divide a D y D divide a 100?

3

Se quieren reemplazar los signos de pregunta por dígitos, de manera que sea válida la cuenta expresada:

1? · 2? · 3? · 4? = N

¿Qué valor debe tener N para que la cantidad de formas posible sea máxima?

Nota: Es posible que se repitan dígitos. Por ejemplo para N=315084 hay dos formas:

11·21·31·44 = 315084     y     11·22·31·42 = 315084

Archivo de Enunciados CyM Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar