
30 de septiembre de 2005
a) Encontrar tres números enteros X; Y; Z, todos mayores que 2, tales que
X3 + Y3 = Z3 - 1
b) Encontrar tres números enteros A; B; C, todos mayores que 2, tales que
A3 + B3 = C3 + 1
A un tablero cuadrado y cuadriculado, se le recortan tres cuadrados de esquinas distintas, siguiendo las líneas del cuadriculado. Después de haber sacado los tres cuadrados, quedan 2005 casilleros. Calcular el tamaño del tablero más chico con el que se puede hacer esto

¿Cuántos números primos de 5 cifras son
de la forma PPPQQ, con P distinto de Q? O sea que las tres
primeras cifras son iguales entre sí, y las dos últimas
también son iguales entre sí, pero distintas de las otras.
Nota: Un número entero positivo es primo cuando solamente es
divisible por 1 y por sí mismo, y no es el número 1. Por
ejemplo 2, 3, 5, 7, 11, 13, ... son primos, mientras que 245 no
lo es, porque es divisible por ejemplo por 5.
Encontrar todas los pares de números de
cuatro cifras de la forma (R2D2 ; C3PO) tales que R2D2 * C3PO es
un número que termina en 7094.
Nota: O es la letra ‘O’, no es un 0 (cero).
Se define la sucesión TiK(n) de la siguiente manera:
TiK(1) := 2;
TiK(n+1) := el primer primo en la sucesión f(TiK(n)),
f(f(TiK(n))), f(f(f(TiK(n)))),
…
donde f(k): = 2 · k + 1.
Calcular todos los términos TiK(n) de la sucesión tales que TiK(n) < 232.
Por ejemplo TiK(5) = 47 y entonces TiK(6) = 191, porque f(TiK(5)) = f(47) = 95 que no es primo y f(f(TiK(5))) = f(f(47)) = f(95)=191 que es primo.
a) ¿Cuántos triángulos distintos hay,
que tengan todos los lados enteros y perímetro 48?
b) ¿Y con perímetro 95?
c) ¿Y con perímetro 96?
d) ¿Y con perímetro 2005?
No importa el orden de los lados de un triángulo. Consideramos al triángulo de lados 4; 5; 8 igual que el triángulo de lados 8; 5; 4. Tampoco consideramos válidos a los "triángulos degenerados", o sea, los que corresponderían a tres puntos alienados.
Nota: Tres segmentos no siempre forman triángulo. Por ejemplo 20; 3; 4 no son los lados de un triángulo.
Un numero es superimpar si todas sus
cifras son impares.
Cuáles son todos los múltiplos de 367 que tienen exactamente 5
cifras y son superimpares.
Dos números M y N (M < N) se dicen amigables si la suma de los divisores propios de M es igual a N, y recíprocamente, la suma de los divisores propios de N es igual a M.
Hallar todos los pares de enteros positivos amigables menores que 15000.
Nota: Los divisores propios de un número A son los divisores positivos distintos del mismo A. Por ejemplo, los divisores propios de 6 son 1, 2 y 3, y su suma es 6.
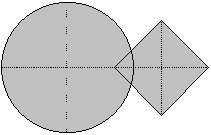
Se tiene un círculo de radio 1 y un cuadrado de lado 1, colocados de manera tal que la prolongación de una diagonal del cuadrado pasa por el centro del círculo. Además están ligeramente superpuestas, así que la superficie cubierta por ambas figuras es 4.
Aproximar la distancia entre el centro del círculo y el centro del cuadrado, con un error menor de 0,001.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |