8mo
Torneo de Computación y Matemática
Primera
Ronda
26 de agosto de 2005
Nivel 1 (7mo y 8vo año de escolaridad)
Encontrar cuatro números enteros X; Y; Z; W, todos entre 10 y 20, tales que
X · Y + Z · W = 539
Hallar un número entero mayor que 1; que sea divisor de 24272 y que también sea divisor de 25461.
Se eligen tres números enteros positivos distintos. La diferencia entre el mayor y el menor es justo 30. Además si se los multiplica a los tres números elegidos se obtiene 217140. ¿Cuáles son esos números?
Nivel 2 (9no y 10mo año de escolaridad)
La ecuación
tiene muchas soluciones en las que X;
Y; Z son números enteros mayores que 1, por
ejemplo:
X = 2;Y = 4; Z = 3
X = 2;Y = 2; Z = 6
X = 3;Y = 3; Z = 3
X = 4;Y = 2; Z = 4
Encontrar otras dos soluciones con números enteros mayores que
1, que no sean ninguna de las nombradas.
Encontrar tres números enteros, el primero de 1 cifra, el segundo de 2 cifras y el tercero de 3 cifras, tales que al multiplicarlos se obtiene 396865
Cada día se agregan 5000 litros de agua a una pileta que inicialmente esta vacía. Por la noche pierde un 10% (debido al agua que toman los murciélagos). ¿Cuántos días hay que esperar para que al llegar por la mañana la pileta tenga por lo menos 40000 litros?
Nivel 3 (11er año de escolaridad en adelante)
Buscar un número ABCDE de 5 cifras, todas distintas de 0, tal que ABCDE sea múltiplo de 19, ABCD sea múltiplo de 29 y BCD sea múltiplo de 39.
Buscar el máximo de la función
.gif)
cuando x toma todos los valores
enteros entre 1 y 1000.
Dar el valor de x (exacto) y f(x) (aproximado).
La siguiente tabla
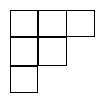
se puede llenar poniendo 1, 2, 3, 4, 5, o 6
en cada casilla de manera que en cada fila los números no
decrezcan, y en cada columna los números vayan creciendo
estrictamente.
Por ejemplo
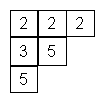
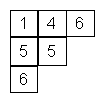
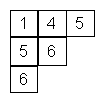
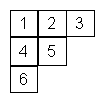
¿De cuántas maneras distintas se puede llenar la tabla cumpliendo estas reglas?
 Archivo de Enunciados CyM Página Principal |
Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
| mensajes webmaster@oma.org.ar |