1 de octubre de 2004
Encontrar cuatro números enteros positivos
x, y, z, w , todos distintos de 1, tales que
x + x * y + x * y * z + x * y * z * w = 3239
Numerobis elige un numero n entero
positivo, lo multiplica por 0,8 y le toma la parte entera y luego
anota cuidadosamente este resultado en un papel.
Al resultado lo multiplica por 0,8 y le toma la parte entera y
anota el nuevo resultado en el mismo papel.
A este nuevo resultado lo multiplica por 0,8 y se le toma la
parte entera y se escribe el valor así obtenido junto a los
otros dos.
Al calcular la suma de los tres números anotados obtiene 2004.
¿Cuál fue el numero n que eligió originalmente? ¿Hay más de
una posibilidad?
Nota: La parte entera de 17,1367 es 17; la parte entera de
45,9999 es 45; la parte entera de 12 es 12.
Decimos que un número es musical si tiene
8 cifras, de las cuales la primera, la tercera y la última son
impares, y las otras cinco son pares. Por ejemplo, 18250245 es un
número musical.
Decimos que un número es simple si se escribe con 2 cifras: 32,
322 o 23232 son simples, mientras que 2, 234 o 22 no son simples.
Un número entero positivo es primo cuando solamente es divisible
por 1 y por sí mismo, y no es el número 1. Por ejemplo 2, 3, 5,
7, 11, 13, ... son primos, mientras que 18250245 no lo es, porque
es divisible por ejemplo por 5.
Encontrar un número que sea al mismo tiempo primo, simple y
musical.
Se buscan los pares de enteros positivos
(X,Y), tales que el numero
x2 × y + 8 × x × y + 4 × y2
empieza con 8 y termina con 3
a) ¿Cuáles son los pares en que x e y son ambos menores
que 100?
b) ¿Cuántos son los pares en que x e y son ambos menores
que 1000?
Nota: Por ejemplo 820043 es un número que empieza con 8 y
termina con 3.
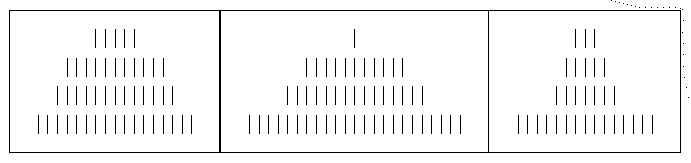
El Nim es un popular juego para dos jugadores, que tiene muchas variantes. En todas ellas el "tablero" consiste en varias filas con una cantidad impar de palitos, la fila superior con menos palitos y la inferior con más. Cada fila tiene estrictamente más palitos que la fila inmediatamente superior. Y todas las filas tienen por lo menos un palito. También puede variar la cantidad de filas.
En la variante que consideramos hay 4 filas, y cada una de ellas puede tener hasta 85 palitos inclusive (Ver figura). ¿Cuántos "tableros" posibles hay?

Para cada valor fijo de k el conjunto de
puntos
{ (x,y): x2 - y2 = k }
es una hipérbola distinta. Hallar un valor de k entero positivo
menor o igual que 10000 tal que la cantidad de soluciones de x2-
y2 = k con x e y enteros no negativos sea máxima.
Para cada entero positivo R se definen los
tres siguientes números:
S(R)= La superficie del circulo de Radio R y centro (0,0)
D(R)= La cantidad de puntos (x,y) que están en el circulo de
radio R y centro (0,0) (incluyendo el borde), tales que x e y son
números enteros.
E(R)=S(R)-D(R)
Considerando los valores que toma E(R) cuando R está entre 1 y
1000 (inclusive), encontrar su valor mínimo y máximo.
Se define la sucesión an de la
siguiente manera:
a1 = 2449
an+1 = SacarPrimeraDe(12 × an)
en donde si N es un número entero positivo,
SacarPrimeraCifraDe(N) es el número que se obtiene al sacar su
primera cifra no nula. Por ejemplo SacarPrimeraCifraDe(245)=45,
SacarPrimeraCifraDe(0028)=8 , SacarPrimeraCifraDe(3)=0.
La sucesión comienza así:
2449 ->9388-> 12656-> 51872-> 22464-> 69568->
34816-> 17792-> 13504->....
o sea que el 13504 ocupa el noveno lugar.
Buscar en que posición aparece el primer 2.
Una octava son 8 números enteros positivos
separados de a 6, o sea x, x + 6, x + 12,
..., x + 42 tales que el primero (x), el cuarto (x+18)
y el octavo (x+42) no son primos, y los otros cinco sí son
primos.
a) Encontrar la primer octava (o sea, encontrar el menor x entero
positivo tal x, x + 6, x + 12, ...,
x + 42 es una octava).
b) Encontrar la segunda y la tercera.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |