6to
Torneo de Computación y Matemática
Segunda
Ronda
19 de septiembre 2003
Nivel 1 (7mo y 8vo año de escolaridad)
1
Buscar dos números enteros positivos X e Y tales que X · Y · (X + Y) = 445500
2
Se consideran todos los números enteros de
cinco cifras de la forma 5A1A3 en donde A es
una cifra. (Las dos veces que aparece A representa la
misma cifra). ¿Hay alguno que sea un número primo?
Nota: Los números primos son los que tienen como únicos
divisores al 1 y a sí mismos, por ejemplo 2, 3, 5, 7, 11, 13,
...
3
Se compraron dos cajas con la misma cantidad de figuritas. Se sabe que en cada caja hay menos de 1000 figuritas. La primera caja se repartió entre los 30 alumnos de una división, de manera que a cada uno le toco la misma cantidad de figuritas, y sobraron 11. Con el mismo método se repartió la segunda caja entre los 37 alumnos de la otra división y sobraron 5 figuritas. ¿Cuántas figuritas había en la caja?
Nivel 2 (9no y 10mo año de escolaridad)
1
Buscar un número entero positivo mayor que
1000 que sea primo y además empiece con 90 y termine con 51.
(Por ejemplo 90948051 es un número que empieza 90 y termina con
51.)
Nota: Los números primos son los que tienen como únicos
divisores al 1 y a sí mismos, por ejemplo 2, 3, 5, 7, 11, 13,
...
2
Encontrar tres números enteros positivos X; Y y Z , tales que (X + Y) · (Y + Z) · (Z + X) = 83334
3
En un negocio venden alfajores sueltos por
mayor, así que hacen un descuento por cantidad. Si se compran N
alfajores juntos el precio de cada uno es de pesos
1 - N/1000 + N2 / 2000000 . Por ejemplo si se compran
150 alfajores se debe pagar $129,1875 La máxima cantidad de
alfajores que se puede comprar es 1000. ¿Cuántos alfajores se
podrá comprar con $300?
Nota: En este negocio hacen todas las cuentas sin redondear los
valores.
Nivel 3 (11er año de escolaridad en adelante)
1
Buscar dos números enteros positivos de
cuatro cifras ABCD y EFGH que sean primos y tales
que el número de ocho cifras ABCDEFGH también sea primo.
Nota: Los tres números que aparecen pueden tener cifras
repetidas.
2
Para cada entero positivo de n se
considera la siguiente ecuación: X2 + n
· Y4 = Z2 en donde X;
Y y Z son números enteros positivos y Z es
menor que 1000. Para cada valor fijo de n se buscan todas
las soluciones y se las cuentan. ¿Cuál es el valor de n
en el que se encontraron más soluciones?
Nota: El cero no es un número positivo.
3
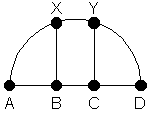
Se tiene un semicírculo de diámetro AD = 100. Se lo divide en tres pedazos de igual área usando los segmentos BX y CY que son perpendiculares a AD. Calcular la longitud de BC con un error menor que 0,01.

| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |