6^to Torneo de Computación y Matemática
Primera Ronda

8 de agosto 2003

Nivel 1 (7^mo y 8^vo año de escolaridad)

1

Encontrar cuatro números enteros positivos A; B; C y D tales que A² + B² + C² + D² = 35296
Nota: El cero no es un número positivo.

2

Se toman dos números enteros positivos de 4 cifras A y B. Al calcular su producto se obtiene 45671238. Hallar todos los posibles valores de A y B, sabiendo que A es impar.
(por ejemplo si A=5861 y B=4867 entonces A · B vale 28525487 y no sirven)

3

Para una fiesta se compran tres tipos de bebidas. Una botella de Supercola trae 747 cm³ y cuesta $1,34. Una botella de Manzanín trae 848 cm³ y cuesta $1,15. Una botella de Aguachento trae 696 cm³ y cuesta $0,95. Si en total se compraron 24101 cm³ de bebida, ¿cuánto se debió pagar?

Nivel 2 (9^no y 10^mo año de escolaridad)

1

Sean A; B y C tres números enteros positivos tales que 20 · A + 3 · B + 2003 · C = 21633600. Además B es múltiplo de A y también se sabe que C es múltiplo de B. Encontrar todas las posibilidades.

2

En un juego se elige un número entero positivo A de cinco cifras. El puntaje es igual a la suma de los dígitos de 2003·A. Por ejemplo si se toma un valor de A de 31415 se obtienen 34 puntos. ¿Cuál es el máximo puntaje que se puede obtener en este juego?

3

Buscar un número entero positivo distinto de 1, que sea divisor de 2030275616 y que tenga todas sus cifras impares.

Nivel 3 (11^er año de escolaridad en adelante)

1

Un número entero positivo es suertudo cuando la suma de sus cifras es 7 (por ejemplo 7; 133; 700; 1111111; ... )

Encontrar el menor número entero positivo que tenga por lo menos siete divisores positivos suertudos distintos.

2

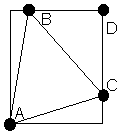
Se tiene un campo rectangular, A y D son dos de sus vértices, B y C son dos puntos de sus lados, como en la figura.
Se sabe que la distancia de A a C es , la distancia de B a C es y la de A a B es .
Además se sabe que la longitud de los lados del campo son un número entero, y la distancia de B a D y la distancia de C a D son también enteros.
Hallar la longitud de los lados del campo.

3

Para cada número entero positivo n llamamos D(n) al mayor divisor de n que es distinto de n.
Por ejemplo D(100) = 50; D(1729) = 247; D(2003) = 1.
Calcular D(2)+D(3)+D(4)+... +D(99998)+D(99999)+D(100000).

Archivo de Enunciados CyM Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar