5to
Torneo de Computación y Matemática
Ronda
Final
Capital Federal, 4 al 6 de diciembre de 2002
Nivel 1 (7mo y 8vo año de escolaridad)
Primer día
1
a) Encontrar dos números enteros positivos
a y b que verifiquen a2 =
3001 + b2
b) Encontrar dos números enteros positivos c y d
que verifiquen c2 = 30013 + d2
2
Se tienen 1000 litros de aceite para envasar en barriles de 43 litros y/o bidones de 47 litros. Todos los barriles y bidones que se usen se deben llenar completamente. Hallar una combinación de recipientes de modo que se deje sin envasar la menor cantidad de aceite posible.
3
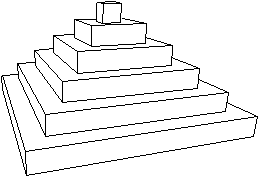
El zigurat de Nahr-Zaggrond es similar a una pirámide. Está construido con bloques cúbicos de 76cm de lado. Los bloques están dispuestos en pisos cuadrados. Cada piso tiene dos bloques menos, por lado, que el piso inmediatamente inferior. El piso superior tiene un solo bloque. La pirámide tiene 38m de altura. ¿Cuántos bloques constituyen el zigurat?
Segundo día
4
a) Buscar dos números enteros positivos x,
y tales que 911 · x + 119 · y = 514271
b) ¿Es posible encontrar una solución en que x e y
sean ambos capicúas?
5
Encontrar un número entro positivo n
que tenga 14 divisores y que además n+2 tenga 18
divisores.
Nota: Los divisores de 12 son: 1,2,3,4,6,12.
6
Matías toma un número de 4 cifras, todas
distintas de cero, y le saca la primera (más significativa),
después le saca la segunda, y por último la tercera. Así
obtiene 4 números de 4, 3, 2 y 1 cifra, respectivamente. Al
multiplicarlos obtiene 452100096. ¿De qué número empezó? Dar
todas las posibilidades.
Ejemplo: si empezamos con 7231 tenemos 7231*231*31*1 que da
51781191, así que 7231 no sirve.
Nivel 2 (9no y 10mo año de escolaridad)
Primer día
1
En un bosque se numeran los árboles del 1
al 10000000 (ambos inclusive). Para cada árbol se realiza la
siguiente operación: Primero se escribe el número que le
corresponde. Luego se calcula la suma de las cifras de dicho
número y se lo escribe debajo. Luego se calcula la suma de las
cifras del último número escrito y se escribe el resultado
debajo. Este procedimiento continúa hasta obtener un número de
1 cifra.
Por ejemplo en el árbol 23893 se escribe la siguiente lista
23893, 27, 9. En el árbol 2002 se escriben 2002 y 4. En el
árbol 7 se escribe sólo el número 7.
Los árboles que florecen son aquellos que solamente tienen
escritos números que son múltiplos de 4. ¿Cuántos arboles
florecen?
2
Se factoriza al número 2002! como producto
de primos. Hallar todos los primos que aparecen por lo menos 50
veces en esta factorización.
Aclaración: 2002!=1.2.3.4. ... .2000.2001.2002
3
Es conocido que todo entero positivo se
puede escribir como suma de nueve cubos o menos. Por ejemplo, 343
= 13 + 73, y 72 = 23 + 23
+ 23 + 23 + 23 + 23 +
23 + 23 + 23. Sin embargo, hay
solamente 2 (dos) enteros positivos que requieren de nueve cubos
no nulos. Para todos los demás, ocho o menos son suficientes.
Hallar esos 2 (dos) números.
Segundo día
4
Hallar enteros positivos x, y, z, w tales que 71 · x + 9 · y + 103 · z + 60 · w · w = 1078122 al mismo tiempo que 62 · x + 78 · z = 2002.
5
Se tomó una prueba de matemática a todos
los alumnos de una división, salvo a Fernando y Daniel que
habían faltado. Al calcular el promedio se obtuvo 6,7...
Al día siguiente vino Fernando, se le tomo la prueba y obtuvo 8
puntos. El nuevo promedio de la división fue 6,8...
Un día más tarde vino Daniel, sacó 10 puntos y al recalcular
el promedio se obtuvo 6,9...
Encontrar la cantidad de alumnos que puede tener esa división.
Dar todas las posibilidades.
Nota: Las notas son enteras, el mínimo es 1 y el máximo 10.
6
Lucas quiere encontrar una aproximación a
la raíz cuadrada de 2 mediante una fracción p/q.
Pero además quiere que q no sea un número demasiado
grande. Después de pensarlo un rato y consultarlo con sus amigos
decidió que lo mejor seria que el valor de 
sea lo más chico posible y que q
sea menor que 1000000. Buscar los valores de p y q
que cumplan esta condición.
Nota |x| es el valor absoluto de x, por ejemplo
|5|=5 y |-3|=3.
Nivel 3 (11mo año de escolaridad en adelante)
Primer día
1
Factorizar 5110 - 3 · 574 + 75 · 536 - 25 como un producto de primos.
2
¿Es posible armar dos dados de seis caras,
usando 12 enteros positivos distintos, de manera que todos los
resultados posibles sean primos? En caso afirmativo, dar un
ejemplo. En caso negativo, demostrarlo.
(El resultado de tirar dos dados es la suma de las caras
superiores. Los números se escriben en las caras con dígitos
chiquitos, no con puntitos.)
3
Un número es amarilloso si la suma de sus
divisores positivos (incluidos 1 y si mismo) es 2002002002.
a) Hallar algún número amarilloso.
b) Hallar todos los números amarilloso.
Segundo día
4
Hallar todas las potencias de 5 que en su expresión decimal no tienen dos dígitos consecutivos iguales y todos sus dígitos son pares salvo el ultimo de la derecha. Por ejemplo, 25.
5
Pablo dibuja un pentágono inscripto en una circunferencia, cuyos lados son 11, 13, 17, 19 y 23, (en este orden) hallar el radio de la circunferencia. (Dar la respuesta con un error menor que 0,00001).
6
Sea F0 = 0, F1
= 1, Fn = Fn-1
+ Fn-2 si n>1, la
sucesión de Fibonacci. Por ejemplo F2=1, F3=2,
F4=3, F5=5, F6=8.
i) Hallar tres funciones a(n), b(n),
c(n) lineales y dos funciones g(n),
h(n) tales que valga que para todo n>0,
0 · F0 + 1 · F1
+ 2 · F2 + ... + n · Fn
= a(n) · Fg(n)
+ b(n) · Fh(n)
+ c(n)
Una función es lineal cuando es de la forma d(n) = s · n + t
ii) Demostrarlo.
 Archivo de Enunciados CyM Página Principal |
Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
| mensajes webmaster@oma.org.ar |