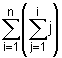
5to
Torneo de Computación y Matemática
Segunda
Ronda
30 de agosto de 2002
Nivel 1 (7mo y 8vo año de escolaridad)
1
Hallar algún divisor de 2130978874 entre 1000 y 2000.
2
Encontrar tres números enteros positivos x, y, z tales que 213 · x + 137 · y + 177 · z = 3286536 y además x sea múltiplo de 4, y múltiplo de 10 y z múltiplo de 9.
3
Un avión modelo AB529-350
debe volar desde Ushuaia hasta Formosa (4151km) en menos de 5 hs
y media. El tanque de dicho avión contiene 23912 litros de
combustible.
Volando a velocidad constante V (en km/h), la fórmula
que determina el consumo de combustible del modelo AB529-350 es V2
/ 16 - 105 · V + 44500, que indica cuántos litros de
combustible necesita para recorrer 100 km. Este modelo puede
alcanzar hasta 912 km/h.
Hallar alguna velocidad a la que el avión pueda hacer dicho
viaje.
Nivel 2 (9no y 10mo año de escolaridad)
1
Encontrar dos entero positivos n y z tales que 2n + 5089 = z2.
2
Un divisor d de 3683488 es un superdivisor si la suma de las cifras de d también divide a 3683488. Encontrar todos los superdivisores de 3683488.
3
Definimos el sumarial de n
como 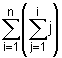
Por ejemplo, el sumarial de 5 es: (1) + (1+2) + (1+2+3) + (1+2+3+4) + (1+2+3+4+5) = 35.
Definimos g(k)
como el resto de sumarial de k al dividirlo por k+1,
por ejemplo g(5) vale 5, que es el resto de la división entera
de 35 por 6.
Definimos además f(n) como 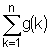 , por ejemplo f(5)
es 1 + 1 + 2 + 0 + 5 =9
, por ejemplo f(5)
es 1 + 1 + 2 + 0 + 5 =9
i) Hallar f(148).
ii) Hallar f(4003).
Nivel 3 (11er año de escolaridad en adelante)
1
Hallar todos los conjuntos de 4 números enteros positivos {a, b, c, d} tales que a2 + b2 + c2 + d2 = 1327104. Nota: Los cuatro números del conjunto deben ser distintos, por supuesto.
2
Se consideran todos los números que se
obtienen reordenando las cifras de 12345678.
a) Encontrar alguno con cantidad de divisores menor o igual a la
de todos los demás.
b) Encontrar alguno con cantidad de divisores mayor o igual a la
de todos los demás.
Ahora se consideran todos los números que
se obtienen reordenando las cifras de 123456789.
c) Encontrar alguno con cantidad de divisores menor o igual a la
de todos los demás.
3
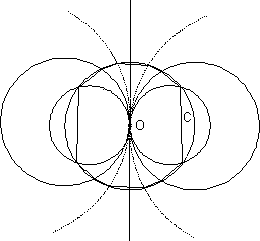
Sobre una recta se marca el punto O. Se traza la circunferencia C de centro O y radio 2000. Se trazan circunferencias tangentes a la recta en el punto O, de ambos lados, y de radios 1001, 1002, 1003, ..., 2001, 2002, las cuales cortan a la circunferencia C en determinados puntos. Calcular el área del polígono convexo inscripto en C con vértices en dichos puntos.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |