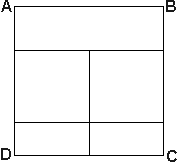
El área de cada uno de los cuadrados es a y el área de cada uno de los dos rectángulos más pequeños es b. Si a + b = 24 y la raiz cuadrada de a es un número natural, hallar todos los valores posibles del área del cuadrado ABCD.
VII
Olimpíada Matemática del Cono Sur.Perú. 1996
Primer
día| 1. Un cuadrado
ABCD se divide en dos cuadrados y tres
rectángulos, como se muestra en la figura: El área de cada uno de los cuadrados es a y el área de cada uno de los dos rectángulos más pequeños es b. Si a + b = 24 y la raiz cuadrada de a es un número natural, hallar todos los valores posibles del área del cuadrado ABCD. |
 |
2. Considerar una sucesión de números reales definida por:
an + 1 = an + 1/an para n = 0, 1, 2, ...
Demostrar que, cualquiera que fuera el número real positivo a0, se cumple que a1996 es mayor que 63.
3. Una tienda vende envases con las siguientes capacidades: 1 litro, 2 litros, ... 1996 litros. Los precios de los envases satisfacen las dos condiciones siguientes:
Hallar todos los pares de envases de m y n litros tales que:
NOTA: Las operaciones permitidas para medir son:
Se ha logrado medir k litros cuando la cantidad de litros de un envase mas la cantidad de litros del otro, es igual a k.
Segundo
día4.
La sucesión 0, 1, 1, 1, ... , 1 contiene 1996
números, siendo el primero cero y todos los demás unos.
Se eligen dos o más números cualesquiera de la
sucesión (pero no toda la sucesión) y se sustituye uno
de ellos por la media aritmética de los números
elegidos, obteniéndose así una nueva sucesión de 1996
números.
Probar que, con la repetición de esta operación, es
posible obtener una sucesión en la cual los 1996
números son iguales.
NOTA: En cada operación no necesariamente se debe elegir
la misma cantidad de números.
5. Se pretende cubrir
totalmente un cuadrado de lado k (k
entero mayor que uno) con los siguientes rectángulos: 1
rectángulo de 1 x 1, 2 rectángulos de 2 x 1, 4
rectángulos de 3 x 1, ... , 2n rectángulos
de (n+1)x1, de tal manera que los rectángulos no se
superpongan ni excedan los límites del cuadrado.
Hallar todos los valores de k para los cuales esto
es posible y, para cada valor de k encontrado,
dibujar una solución.
6. Hallar todos los
números enteros n ![]() 3 tales que exista un
conjunto Sn formado por n puntos del plano que
satisfagan las dos condiciones siguientes:
3 tales que exista un
conjunto Sn formado por n puntos del plano que
satisfagan las dos condiciones siguientes:
NOTA: Los puntos de la circunferencia no se consideran interiores al círculo.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |