Bolivia. 1995

1. Hallar un número de tres cifras, sabiendo que la suma de sus cifras es 9, el producto de las mismas es 24 y además el número leído de derecha a izquierda es 27/38 del número primitivo.

2. Hay diez puntos marcados sobre una circunferencia. Los numero del 1 al 10 y trazo todos los segmentos que estos puntos determinan. Coloreo los segmentos, unos con rojo y otros con azul. Sin cambiar los colores de los segmentos, renumero todos los puntos del 1 al 10.
¿Será posible colorear los segmentos y renumerar los puntos de modo que aquellos números que estaban unidos con rojo queden ahora unidos con azul y los números que estaban unidos con azul queden ahora unidos con rojo?.

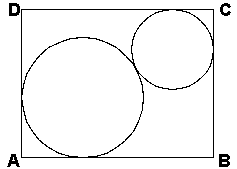
3. Sea ABCD un rectángulo cuyos lados miden AB=a y BC=b. Dentro del rectángulo se trazan dos circunferencias tangentes exteriormente de manera que una es tangente a los lados AB y AD y la otra es tangente a los lados CB y CD. Calcular la distancia entre los centros de las circunferencias en función de a y b. Haciendo variar los radios de modo que la situación de tangencia se mantenga, el punto común de las circunferencias describe un lugar geométrico. Determinar este lugar geométrico.

Segundo día

4. Se escribe las cifras de 1995 como sigue:

199511999955111999999555......

1. Calcular cuántos dígitos se deben escribir para que la suma de los dígitos escritos sea 2880.

2. Determinar el dígito que aparece en el lugar 1995.

5. La semicircunferencia de centro O y diámetro AC se divide en dos arcos AB y BC en la relación 1:3. M es el punto medio del radio OC. Sea T el punto del arco BC tal que el área del cuadrilátero OBTM es máxima. Calcular dicha área en función del radio.

6. Sea n natural, sea

f(n) = 2n - 1995 [n/1000]

Donde [ ] denota la función parte entera.

1. Demostrar que si para algún r, f( f( f...f(n)...)) = 1995 (donde se aplica r veces la función f), entonces n es múltiplo de 1995.

2. Demostrar que si n es un múltiplo de 1995, existe un r tal que f( f( f...f(n)...)) = 1995 (donde se aplica r veces la función f). Determinar r si n = 1995 x 500 = 997500.

Aclaración: Parte entera de un número x, es el mayor número entero que es menor o igual a x.
Por ejemplo: [3,2] = 3; [4] = 4; [-2,5] = -3.

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar