II Olimpíada Matemática del Cono Sur

Argentina. 1991

1

Sean A, B y C tres puntos no colineales (no alineados) y E (B) un punto cualquiera que no pertenezca a la recta AC. Construya los paralelogramos ABCD (en este orden) y AECF (también en este orden). Demuestre que BE // DF.

2

Dos personas A y B juegan el siguiente juego: A comienza eligiendo un número natural y luego, cada jugador en su turno, dice un número de acuerdo con la siguiente regla:

• si el último número dicho fue impar, el jugador suma 7 a este número;
• si el último número dicho fue par, el jugador lo divide por 2.

Gana el jugador que repite el número que fue elegido inicialmente. Encontrar todos los números que A puede elegir para ganar. Justifique la respuesta.

3

Se sabe que el número de soluciones reales del siguiente sistema es finito. Pruebe que este sistema tiene un número par de soluciones:

(y² + 6) (x - 1) = y (x² + 1)

(x² + 6) (y - 1) = x (y² + 1)

4

Un juego consiste de 9 botones (de color negro o blanco) dispuestos de la siguiente manera:

Si se aprieta un botón del borde del cuadrado cambian de color él y todos sus vecinos, si se aprieta el botón del centro cambian de color sus 8 vecinos pero él no.
Los ejemplos siguientes muestran con círculos -blancos- los botones que cambian de color al presionar el botón que se indica.

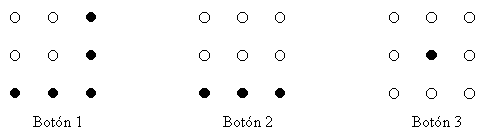
¿Es posible (apretando sucesivamente algunos botones) dejar todos los botones con color negro, si inicialmente estaban todos de blanco? Justifique su respuesta.

5

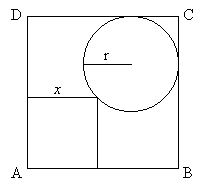
Dado un cuadrado ABCD de lado 1, y un cuadrado interior de lado x, hallar (en función de x) el radio de la circunferencia que es tangente a dos de los lados del cuadrado ABCD y que pasa por un vértice del cuadrado interior, tal como se indica en la figura.

6

Dado un número natural n (diferente de 0), sea f(n) el promedio de todos sus divisores positivos. Por ejemplo:

f(3) = (1+3)/2 = 2
y
f(12) = (1+2+3+4+6+12)/6 = 14/3

1. Demuestre que:

2. Encuentre todos los números naturales n para los cuales:

f(n) = 91/9

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar