XII Olimpíada Matemática del Cono Sur
Prueba de Selección

19 y 20 de abril de 2001

1

Sean a, b, c, d dígitos, con a distinto de 0, tales que 0,abc = a / (b + c + d)

Hallar todos los valores posibles de a, b, c, d.

2

Sea ABC un triángulo rectángulo en C. Se consideran D en la hipotenusa AB tal que CD es altura del triángulo, y E en el cateto BC tal que AE es bisectriz del ángulo A. Si F es el punto de intersección de AE y CD, y G es el punto de intersección de ED y BF, demostrar que

área (CEGF) = área (BDG).

3

Un herrero fabrica rejas cuadradas cuadriculadas en cuadraditos de 1 dm de lado (en la figura se muestra el ejemplo de la reja de 5x5). Para ello dispone de barras metálicas de 2 dm, de barras metálicas de 1 dm y de una soldadora. Tiene prohibido superponer barras, ni siquiera cruzarlas de modo que sólo se superpongan en un punto. Al herrero le conviene utilizar la menor cantidad posible de barras de 1 dm.

Determinar para cada número natural n el mínimo número de barras de 1 dm que debe utilizar para fabricar la reja cuadriculada en n x n cuadraditos.

Están permitidas:

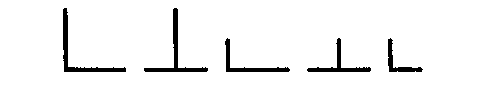
Están prohibidas:

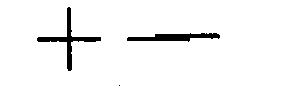
4

Del entero positivo n se sabe que:

• n no es múltiplo de 5,
• n - 96 es múltiplo de 128,
• n tiene 2001 dígitos,
• todos los dígitos de n son pares,
• la suma de los dígitos de n es 2 . 2001 - 4 = 3998,
• la suma de los cuadrados de los dígitos de n es 4 . 2001 = 8004.

Hallar n.

5

Sobre la recta r Pablo marca, de izquierda a derecha, los puntos A, B, C y D. Lucas debe construir, con regla y compás, un cuadrado PQRS, de lados PQ, QR, RS y SP, contenido en uno de los semiplanos determinados por la recta r, de modo que A pertenezca a la recta PQ, B pertenezca a la recta RS, C pertenezca a la recta QR y D pertenezca a la recta SP.

Mostrar un procedimiento que siempre le permita a Lucas hacer la construcción y justificar porqué con dicho procedimiento se logra el cuadrado pedido.

6

Dos jugadores, A y B, juegan por turnos: A tiene los turnos impares (1, 3, 5, 7, ...) y B tiene los turnos pares (2, 4, 6, 8, ...). Cada jugador, en su turno, escribe en el pizarrón el número del turno ó menos el número del turno: primero A escribe 1 ó -1, luego B escribe 2 ó -2, a continuación A escribe 3 ó -3, en seguida B escribe 4 ó -4, etc. El juego termina cuando el último número escrito es múltiplo de 2001, o la suma de los dos últimos números escritos es múltiplo de 2001, o la suma de los tres últimos números escritos es múltiplo de 2001, ..., o la suma de todos los números escritos es múltiplo de 2001. Determinar cuál de los dos jugadores tiene estrategia ganadora; dar dicha estrategia y demostrar que con esa estrategia siempre gana.

ACLARACIÓN: Los múltiplos de 2001 son los números de la forma a . 2001, donde a es un entero que puede ser positivo, negativo o cero.

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar