X Olimpíada Matemática del Cono Sur

20 y 21 de Mayo de 1999

1

Hallar el menor entero positivo n tal que las 73 fracciones

sean todas irreducibles.

2

Sea ABC un triángulo rectángulo en A. Construir el punto P en la hipotenusa BC, tal que si Q es el pie de la perpendicular trazada desde P al cateto AC, entonces el área del cuadrado de lado PQ es igual al área del rectángulo de lados iguales a PB y PC. Mostrar los pasos de la construcción.

3

Hay 1999 bolitas en una fila; algunas son rojas y las demás son azules (podrían ser todas rojas o todas azules). Debajo de cada bolita escribimos un número igual a la suma de la cantidad de bolitas rojas que están a su derecha más la cantidad de bolitas azules que están a su izquierda. Si en la sucesión de números así obtenida hay exactamente tres números que aparecen una cantidad impar de veces, ¿cuáles pueden ser estos tres números?

4

Sea A un número de seis cifras, tres de las cuales están coloreadas y son iguales a 1, 2 y 4.
Demostrar que siempre es posible obtener un número que es múltiplo de 7, efectuando sólo una de las siguientes operaciones: o bien suprimir las tres cifras coloreadas, o bien escribir todas las cifras de A en algún orden.

5

Se da un cuadrado de lado 1. Demostrar que para cada conjunto finito de puntos en el contorno del cuadrado se puede hallar un vértice del cuadrado con la siguiente propiedad: la media aritmética de los cuadrados de las distancias desde dicho vértice a los puntos del conjunto es mayor o igual que 3/4.

6

Una hormiga camina por el piso de un patio circular de radio r y avanza en línea recta, pero a veces se detiene. Cada vez que se detiene, antes de reanudar la marcha, gira 60° alternando el sentido (si la última vez giró 60° a su derecha, la siguiente lo hace 60° a su izquierda, y viceversa). Hallar la máxima longitud posible del camino que recorre la hormiga. Demostrar que la longitud hallada es, efectivamente, la mayor posible.

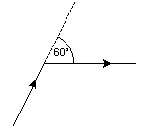
Giro de 60° a la derecha

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar