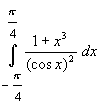
Ronda Final
10 de Diciembre de 1997

Calcular

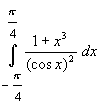
2 (5 puntos)

Sean x₁ , ... , x_n vectores no nulos de un espacio vectorial y f una transformación lineal que satisface:

f(x_i) = x₁ + x₂ + ... + x_i ,      i = 1, .... , n.

Demostrar que los vectores x₁ , ... , x_n son linealmente independientes.

3 (6 puntos)

Una elipse es reflejada en una recta tangente a ella. La imagen de esta reflexión rota sobre la elipse original (que permanece fija) sin deslizarse. Determinar el lugar geométrico de los focos de la elipse que está rotando.

4 (6 puntos)

Sea f(x) una función definida en el intervalo (a,b), estrictamente creciente y cóncava hacia abajo, con derivada continua, tal que para todo x(a,b) se tiene que a<f(x)<x.
Suponga que y sea f_n(x) la n-ésima iterada de f(x) que se define recursivamente por

f₁(x)=f(x) y f_n+1(x)= f_n( f(x)).

Demostrar que

1. (3 puntos) Para toda x(a,b),

2. (3 puntos) Para cualesquiera x,y (a,b),

5 (6 puntos)

Un punto se está moviendo en una recta de tal forma que su velocidad media para cualquier intervalo de tiempo es igual a la media aritmética de las velocidades de los extremos del intervalo. Demostrar que el punto se está moviendo con una aceleración constante.

6 (7 puntos)

¿Es posible dividir una esfera con 4 planos en 15 regiones de igual volumen?

7 (7 puntos)

Llamaremos número 10-ádico a una sucesión infinita de cifras decimales ...a_n...a₁a₀. Los números 10-ádicos se pueden sumar, restar y multiplicar por las mismas reglas que para los números naturales muy grandes. Por ejemplo

   ...1997 +              ...0129 -              ...0129 x

   ...8132                ...8132                ...1997

   -------                -------                -------

   ...0129                ...1997                ....903

                                                 ....61

                                                 ....1

                                                 -------

                                                 ....613

1. (6 puntos) ¿Cuántas soluciones tiene la ecuación x²-x=0 en los números 10-ádicos?
2. (2 puntos) Encontrar la suma de todas las soluciones de esta ecuación.

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar