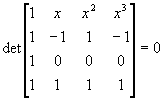
I
Olimpíada Colombiana de Matemática Universitaria.Ronda
Clasificatoria
23
de Octubre de 1997
1 (4 puntos)
Resolver la ecuación
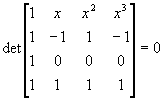
2 (5 puntos)
Una colección de 500 números reales posee la
siguiente propiedad: cualquier número de esta colección
es mayor que 1/5 de la suma de los restantes.
Encontrar la cantidad mínima de números negativos que
pertenecen a la colección.
3 (5 puntos)
Un polinomio p(x) con coeficientes reales es tal que la ecuación p(x)=x no tiene raíces reales. Demostrar que la ecuación p(p(x))=x tampoco tiene raíces reales.
4 (6 puntos)
El área de un trapecio es igual a 2 y la suma de las diagonales es igual a 4. Encontrar la altura del trapecio.
5 (6 puntos)
Hallar todas las funciones reales f(x) definidas en el intervalo [a,b] que tienen las siguientes tres propiedades:
6 (7 puntos)
¿Cuál es mayor, 300! ó 100300?
7 (7 puntos)
Demostrar que cualquier intervalo abierto contiene dos puntos tales que la serie
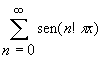
converge en uno de ellos y diverge en el otro.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |