9na Competencia de Clubes Cabri
Segunda Ronda

24 de octubre de 1998

1

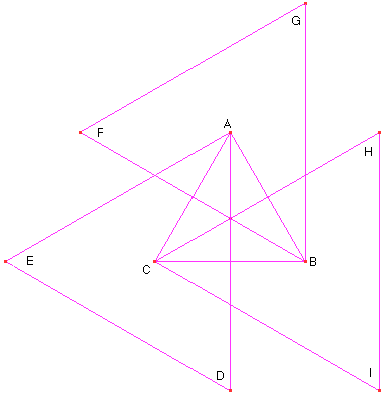
Construir la siguiente figura donde ABC es equilátero y ADE, BFG y CHI son triángulos equiláteros de centros C, A y B respectivamente.

2

Para la figura del problema anterior, hallar el área de DEFGHI si el área de ABC es 303.

3

Dividir un cuadrado en piezas de manera que reacomodando todas esas piezas se pueda formar ocho cuadrados iguales.

4

Dado un paralelogramo ABCD, se construye la circunferencia C circunscripta a ABC de centro O y la circunferencia C’ circunscripta a ACD de centro O’. Probar que OAO’C es un rombo. Justificar.

5

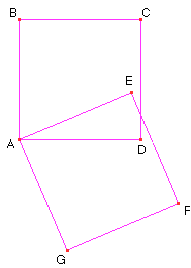
Dado un cuadrado ABCD, construir un cuadrado AEFG.

1. Hallar el lugar geomérico de E para que AEFG sea congruente al cuadrado ABCD.
2. Si AEFG = ABCD, probar que los puntos B, C, F y G están sobre una circunferencia.
3. Hallar el lugar geométrico del centro de dicha circunferencia al variar E sobre el lugar geométrico obtenido en i.
4. ¿Qué tipo de cuadrilátero es BCFG?

6

Dado un rectángulo ABCD y un punto P en AB. Sean E, F y G los baricentros de los triángulo PBC, PCD y PDA respectivamente. Hallar el área de EFG si el área de ABCD es 1998.

7

Sea ABC un triángulo equilátero de centro O. Sea M el punto medio de BC. Trazar la circunferencia de centro P (siendo P el punto de intersección entre la bisectriz de OBC y OM) tangente a AB y AC. Se trazan las rectas BE y CF tangentes a dicha circunferencia en E y F (no pertenecientes a AB y AC), formandose el cuadrilátero ABCD. Hallar los ángulos del mismo.

8

Dado un cuadrado ABCD sea E un punto AB y G un punto CD. Construir el paralelogramo EFGH con F en BC y H en DA.

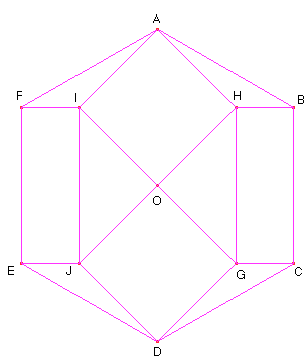
9

Construir la siguiente figura, donde ABCDEF es un hexágono regular de centro O y AIOH, DGOJ son cuadrados:

1. Probar que FIJE y HBCG son rectángulos.
2. Construir un cuadrado de centro O tal que el área del mismo sea la diferencia entre las áreas de AIOH y BCGH. Sugerencia: Trazar las circunferecias circunscritas a BCGH y EFIJ.

Dado un paralelogramo ABCD y un punto P en su interior se trazan los simétricos de P con respecto a AB, BC, CD y DA formándose un cuadrilátero EFGH. Probar que dicho cuadrilátero tiene área fija sin importar la ubicación de P.

10

Sea AB un segmento y P un punto cualquiera. Se construyen los cuadrados MNOP y PQRS de centros A y B respectivamente (QM no corta a AB). Hallar el lugar geométrico de los puntos medios de QM y OS al moverse P por todo el plano.

11

Sea ABCD un cuadrilátero inscripto en una circunferencia. Probar que los incentros de ABC, BCD, CDA y DAB forman un rectángulo.

12

Dado un paralelogramo ABCD y un punto P en su interior se trazan los simétricos de P con respecto a AB, BC, CD y DA formándose un cuadrilátero EFGH. Probar que dicho cuadrilátero tiene área fija sin importar la ubicación de P.

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar