7ma Competencia
de Clubes Cabri
Tercera Ronda
30 de mayo de 1998
| nivel A |
1
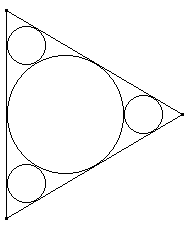
Construir la siguiente figura (el triángulo es equilátero):

Si el círculo pequeño tiene área 5, ¿cuál es el área del círculo grande?
2
Construir un triángulo ABC, tal que si A’, B’ y C’ son los puntos medios de los lados BC, CA y AB respectivamente y se trazan las mediatrices de los segmentos A’B, B’C y C’A, las intersecciones entre estas tres rectas forman un nuevo triángulo congruente al ABC.
3
Dado un paralelogramo ABCD (en ese orden), se traza la recta R paralela a AC que pasa por B. Sea el segmento EF en la recta R de manera que AC y EF miden lo mismo. Probar que ABCD y ACEF tienen el mismo área.
4
Dividir un triángulo equilátero en partes de forma tal que con dichas partes se formen 2 hexágonos regulares iguales.
| nivel B |
5
Dada una circunferencia C y una cuerda AC perteneciente a la misma. Construir el trapecio inscripto ABCD (AB // CD) tal que AC y BD sean perpendiculares.
6
Dada una circunferencia C de centro O y una cuerda AB, sea P la intersección entre la bisectriz de ABO y C. Probar que el circuncentro de PAO pertenece a la circunferencia circunscripta a ABO.
7
Sea ABC un triángulo acutángulo , se construyen los rectángulos semejantes ABDE y BCFG (exteriores al triángulo). Probar que
8
Sea ABCD un trapecio isósceles (AB // CD, AB = BC) de circuncentro O. Probar que BO es bisectriz de ABC.
| nivel C |
9
Dada una circunferencia de centro O y una cuerda AB. Hallar un punto C de la circunferencia de manera que OG = GM (G es el baricentro de ABC y M el punto medio de AB).
10
11
Sea ABC un triángulo. Sea D tal que AD // BC, y E en BC tal que AE // DC. Construir D tal que el ángulo AED sea máximo.
12
Dado un triángulo equilátero ABC hallar el lugar geométrico de O (circuncentro de PBQ) sabiendo que P y Q son puntos de AB y BC tales que PB = QC.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |