7ma Competencia
de Clubes Cabri
Segunda Ronda
16 de mayo de 1998
| nivel A |
1
Dividir un triángulo equilátero en partes de forma tal que
con dichas partes se formen 2 hexágonos regulares iguales.
2
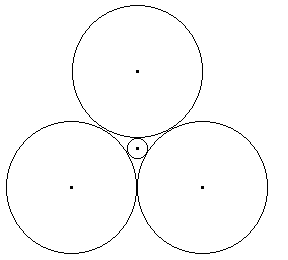
Construir la siguiente figura donde las tres circunferencias grandes tienen el mismo radio y todas las circunferencias son tangentes entre si.

3
Dado un rectángulo ABCD y un punto E en AB construir con regla y con compás el rombo EFGH donde F, G y H pertenecen a BC, CD y DA. Explicar los pasos de la construcción y justificar porque EFGH construido es un rombo.
4
Si en el problema anterior ABCD es un cuadrado, ¿qué figura geométrica es EFGH además de ser rombo? Explicar por qué.
| nivel B |
5
Construir un triángulo ABC dados A, MA (el punto medio de BC) y O (el circuncentro de ABC).
6
Dado un hexágono ABCDEF regular, sea P un punto
en AB. Se trazan r1 y r2
rectas por P perpendiculares a CD y EF
respectivamente. Sea G la intersección entre r1
y BC y H la intersección entre r2
y FA. Probar que AH = GC.
7
Dado un triángulo A1B1C1
cuyo circuncentro es O1, se traza A2B2C2,
el triángulo de los puntos medios de A1B1C1
cuyo circuncentro es O2. Análogamente se
definen A3B3C3
y O3, A4B4C4
y O4, etc. Demostrar que todos los Oi
están alineados.
8
Dado un cuadrado ABCD, sea P un punto en su interior. Se construye el punto E como la intersección (distinta de P) entre las circunferencias de diámetros PA y PC. Se construye el punto F como la intersección (distinta de P) entre las circunferencias de diámetros PB y PD.
- Hallar el lugar geométrico de P para que EF sea máximo.
- Hallar el lugar geométrico de P si EF mide la mitad del lado del cuadrado.
- Hallar el lugar geométrico del punto medio de EF si P es interior al cuadrado.
| nivel C |
9
Dividir un hexágono regular en partes de manera de formar 4 hexágono regulares iguales. ¿Cuál es la menor cantidad de partes?
10
Construir un triángulo isósceles ABC (AB = BC) tal que el triángulo formado por AC y las mediatrices de AB, BC tenga igual área que el triángulo ABC.
11
Sea ABC un triángulo, se trazan las circunferencias CAB, CBC y CCA de centro A que pasa por B, de centro B que pasa por C y de centro C que pasa por A respectivamente. Sea rAC la recta que pasa por las intersecciones de CAB y CBC. Sea rAB la recta que pasa por las intersecciones de CBC y CCA. Sea rBC la recta que pasa por las intersecciones de CCA y CAB. Demostrar que dichas rectas concurren.
12
Dado un cuadrado ABCD, sean MAB, MBC, MCD y MDA los puntos medios de AB, BC, CD y DA respectivamente. Probar que las rectas AMBC y AMCD dividen al segmento MABMDA en tres segmentos iguales.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |