6ta Competencia de Clubes Cabri
Segunda ronda
1er nivel
1. Dividir un triángulo equilátero en seis triángulos isósceles.
2. Hallar el lugar geométrico de los puntos cuyas distancias a dos rectas dadas están en relación 1:2. Justificar
3. Dado un triángulo rectángulo ABC. Sean mA, mB y mC los puntos medios de los lados BC, CA y AB respectivamente. Se trazan CA, CB y CC circunferencias de centros mA, mB y mC que pasan por A, B y C respectivamente. Probar que dichas circunferencias pasan por un mismo punto.
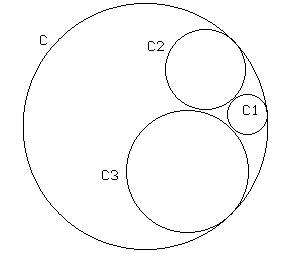
4. Construir la siguiente figura, donde cada circunferencia es tangente a las otras tres y los radios de C1, C2 y C3 están en relación 1:2:3.

2do Nivel
5. Dada una circunferencia C, un punto B en su interior, construir un rombo ABCD, con A y C sobre C y de área máxima.
6. Dado un triángulo ABC. Sea CB el simétrico de C con respecto a B. Sea BC el simétrico de B con respecto a C. Sea AB el simétrico de A con respecto a B. Sea AC el simétrico de A con respecto a C. Sea O el baricentro de ABACBCCB. Probar que las áreas de ABC y OABAC son iguales.
7. Dado un cuadrado ABCD se construyen los triángulos ABE y BCF (exteriores al cuadrado) tales que <EAB = <BCF = 15° y <EBA = <CBF = 30°. Probar que AF, BD y CE se cortan en un punto formado seis ángulos iguales.
8.
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |