4ta Competencia de Clubes Cabri
Primera ronda
1er nivel
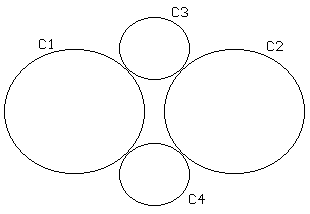
1. Construir la siguiente figura donde C3 y C4 tienen radio la mitad que C1 y C2.

2. Construir el triángulo ABC dados D, E, F tales que: AE / AB = AD / AC = 1 / 4, BF / BC = 1/2.
3. Dado un triángulo equilátero ABC se trazan por A las perpendiculares a AB y AC, por B las perpendiculares a BC y BA y por C las perpendiculares a CA y CB. Hallar la razón entre las áreas de la estrella formada y el triángulo.
4. Dado un círculo C y los puntos A y B en su interior construir un rectángulo inscripto en la circunferencia tal que A y B pertenezcan al perímetro de dicho rectángulo.
5. Analizar la cantidad de soluciones dependiendo de la ubicación de A y B en C.
2do Nivel
6. Construir la siguiente figura donde las tres circunferencias de igual radio estan inscriptas en un cuadrado.
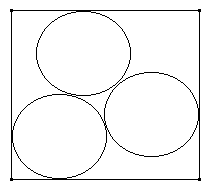
7. Construir un cuadrilátero inscriptible con los lados en relación 1:3:5:7. ¿Es único?
8. Construir el triángulo ABC dados D, E, F tales que: AD / CA = BE / AB = CF / BC = 1/4.
9. Dado un círculo C y un punto P en su interior construir un triángulo equilátero inscripto en la circunferencia tal que P pertenezcan al perímetro de dicho triángulo equilátero.
10. Analizar la cantidad de soluciones dependiendo de la ubicación de P en C.
[ 4ta Competencia - 2da ronda ]
| Olimpíada Matemática Argentina www.oma.org.ar | info@oma.org.ar |
|
| mensajes webmaster@oma.org.ar |