3^era Competencia de Clubes Cabri

Primera ronda

1^er nivel

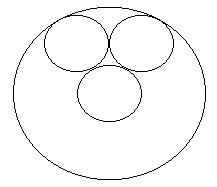
1. Construir la siguiente figura donde las tres circunferencias chicas tienen el mismo radio y una de las circunferencias chicas y la circunferencia grande son concéntricas.

2. Se dan una circunferencia C₁ de centro O, un punto P en ella. Sea C₂ una circunferencia de diámetro OP. Trazar el cuadrado OABC donde A pertenece a C₂ y B pertenece a C₁ (pero no a C₂).

3. Se dan una circunferencia de centro O y un punto A exterior a ella. Construir un rombo ABOC donde B y C son puntos de la circunferencia.

4. Analizar cuándo existe el rombo de la construcción del problema anterior y también cuándo dicho rombo es un cuadrado.

5. Construir un triángulo isósceles ABC (AB = BC) donde la altura desde A (h_A) mide un tercio de la medida de AB.

6. Sea ABC un triángulo equilátero, se traza una circunferencia cuyo diámetro está incluido en AB y es tangente a AC y BC. Se traza la recta r que es paralela a AB y tangente a la circunferencia. Dicha recta interesa a los lados AC y BC en D y E respectivamente. Hallar la relación entre los perímetros de los triángulos ABC y CDE.

7. Se da un hexágono regular ABCDEF. Sea A’ el simétrico de A con respecto a D, sea C’ el simétrico de C con respecto a F, sea E’ el simétrico de E con respecto a B. Sea G el punto medio de DA’, sea H el punto medio de FC’, sea I el punto medio de BE’. Calcular el área del triángulo GHI sabiendo que el área del hexágono regular es 38.

8. Dado un triángulo isósceles ABC (AB = BC), sean r y s las mediatrices de AB y BC respectivamente. Sea D el simétrico de A con respecto a s y sea E el simétrico de C con respecto a r. Hallar la medida del ángulo <DBE en función de la medida del ángulo <ABC.

2^do Nivel

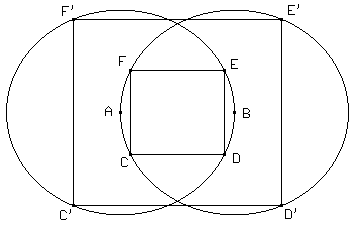
9. Construir la figura, donde CDEF y C’D’E’F’ son cuadrados.

10. Construir un romboide ABCD, (AB = DA, BC = CD), donde los ángulos <B y <D son rectos y (AC / BD)^2 = 2.

11. Inscribir una circunferencia en un cuarto de circunferencia.

12. Dado un triángulo equilátero ABC se trazan r que pasa por A y es perpendicular a AB, s que pasa por B y es perpendicular a BC, t que pasa por C y es perpendicular a CA. Quedándose formado un triángulo equilátero A’B’C’. Calcular la razón entre las áreas de dichos triángulos.

13. Dado un triángulo ABC, se traza la bisectriz r del ángulo C, luego se construye el cuadrado ADBE (en el mismo sentido que ABC). Sea P la intersección entre r y BE. Calcular la relación entre áreas del cuadrado y el triángulo si CP = AD y DB // r.

14. Sea ABCDEFGH un octógono regular, se trazan las rectas AB, CD y GF formándose un triángulo. Demostrar que la relación entre las áreas y los perímetros del triángulo y el octógono regular es la misma.

15. Dado un hexágono regular ABCDEF, construir un cuadrado GHIJ, donde G, H, I, J pertenecen a AB, BC, DE, EF respectivamente.

16. ¿Es único el cuadrado del problema anterior? Justificar.

[ 3era Competencia - 2da  ronda ]

Archivo de Enunciados Página Principal	Olimpíada Matemática Argentina    www.oma.org.ar | info@oma.org.ar
mensajes webmaster@oma.org.ar